题目内容
已知点A（0，2）、B（2
，2）、C（0，4）．
（1）如图1，连接BO、BC、AB．
①填空：AC的长为
②试判断△OBC的形状，并说明理由；
（2）如图2，过点C向右作平行于x轴的射线，点P是射线上的动点，连接BP，以BP为一边在△ABP外侧作等边△BPQ，当四边形ABQP为梯形时，求点P的横坐标．
| 3 |
（1）如图1，连接BO、BC、AB．
①填空：AC的长为
2
2
，AB的长为2
| 3 |
2
；| 3 |
②试判断△OBC的形状，并说明理由；
（2）如图2，过点C向右作平行于x轴的射线，点P是射线上的动点，连接BP，以BP为一边在△ABP外侧作等边△BPQ，当四边形ABQP为梯形时，求点P的横坐标．
分析：（1）①由A、B、C三点的坐标，根据两点间的距离公式即可求出AC=4-2=2，AB=2
；
②运用两点间的距离公式求出OB=4，BC=4，OC=4，根据三边相等的三角形是等边三角形即可得出△OBC是等边三角形；
（2）当四边形ABQP为梯形时，分三种情况进行讨论：①PQ∥AB；②P点与C点重合；③BP⊥CP．
| 3 |
②运用两点间的距离公式求出OB=4，BC=4，OC=4，根据三边相等的三角形是等边三角形即可得出△OBC是等边三角形；
（2）当四边形ABQP为梯形时，分三种情况进行讨论：①PQ∥AB；②P点与C点重合；③BP⊥CP．
解答：解：（1）①∵A（0，2）、B（2
，2）、C（0，4），
∴AC=4-2=2，AB=2
．
故答案为2，2
；
②△OBC是等边三角形．理由如下：
∵O（0，0），B（2
，2），C（0，4），
∴OB=
=4，BC=
=4，OC=4，
∴OB=BC=OC，
∴△OBC是等边三角形；
（2）分三种情况讨论：
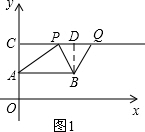
①当PQ∥AB时，如图1．
点Q在CP上，作BD⊥CQ于D，则四边形ABDC是矩形，
∴BD=AC=2，CD=AB=2
．
∵△BPQ是等边三角形，
∴BD平分PQ，平分∠PBQ，
∴PD=BD•tan30°=2×
=
，
∴CP=2
-
=
，
∴点P的横坐标是：
；
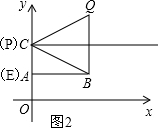②如图2，当P点与C点重合时，
∵在Rt△ABC中，tan∠ABC=
=
=
，
∴∠ABC=30°，
∵∠CBQ=60°，
∴∠ABQ=90°，
∴BQ∥AC，又CQ与AB不平行，
∴四边形ABQP是梯形，
∴点P的横坐标是0；
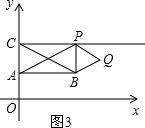③如图3，当BP⊥CP时，
∵CP∥AB，
∴BP⊥AB，
∵在Rt△ABP中，tan∠APB=
=
=
，
∴∠APB=60°．
∵△BPQ是等边三角形，
∴∠PBQ=60°，
∴∠APB=∠PBQ，
∴AP∥BQ，
∴四边形ABQP是梯形，
∴点P的横坐标为2
．
综上所述，四边形ABQP为梯形时，点P的横坐标是
或0或2
．
| 3 |
∴AC=4-2=2，AB=2
| 3 |
故答案为2，2
| 3 |
②△OBC是等边三角形．理由如下：
∵O（0，0），B（2
| 3 |
∴OB=
(2
|
(2
|
∴OB=BC=OC，
∴△OBC是等边三角形；
（2）分三种情况讨论：①当PQ∥AB时，如图1．
点Q在CP上，作BD⊥CQ于D，则四边形ABDC是矩形，
∴BD=AC=2，CD=AB=2
| 3 |
∵△BPQ是等边三角形，
∴BD平分PQ，平分∠PBQ，
∴PD=BD•tan30°=2×
| ||
| 3 |
2
| ||
| 3 |
∴CP=2
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
∴点P的横坐标是：
4
| ||
| 3 |
②如图2，当P点与C点重合时，∵在Rt△ABC中，tan∠ABC=
| AC |
| AB |
| 2 | ||
2
|
| ||
| 3 |
∴∠ABC=30°，
∵∠CBQ=60°，
∴∠ABQ=90°，
∴BQ∥AC，又CQ与AB不平行，
∴四边形ABQP是梯形，
∴点P的横坐标是0；
③如图3，当BP⊥CP时，∵CP∥AB，
∴BP⊥AB，
∵在Rt△ABP中，tan∠APB=
| AB |
| BP |
2
| ||
| 2 |
| 3 |
∴∠APB=60°．
∵△BPQ是等边三角形，
∴∠PBQ=60°，
∴∠APB=∠PBQ，
∴AP∥BQ，
∴四边形ABQP是梯形，
∴点P的横坐标为2
| 3 |
综上所述，四边形ABQP为梯形时，点P的横坐标是
4
| ||
| 3 |
| 3 |
点评：此题考查了两点间的距离公式，等边三角形的判定与性质，解直角三角形，梯形的判定与性质．此题难度适中，解题的关键是根据题意画出符合要求的图形，然后利用数形结合思想求解．
练习册系列答案
相关题目
14、如图，已知点A，B，C在⊙O上，AC∥OB，∠BOC=40°，则∠ABO=
2，A3的横坐标依次为三个连续整数，其他条件不变，求线段CA2的长．