题目内容
【题目】已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为 ![]() 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
的等腰直角三角形DEF的费马点,则PD+PE+PF= .
【答案】![]() +1
+1
【解析】解:如图:等腰Rt△DEF中,DE=DF= ![]() ,
,
过点D作DM⊥EF于点M,过E、F分别作∠MEP=∠MFP=30°,
则EM=DM=1,
故cos30°= ![]() ,
,
解得:PE=PF= ![]() =
= ![]() ,则PM=
,则PM= ![]() ,
,
故DP=1﹣ ![]() ,
,
则PD+PE+PF=2× ![]() +1﹣
+1﹣ ![]() =
= ![]() +1.
+1.
故答案为: ![]() +1.
+1.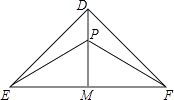
根据题意首先画出图形,过点D作DM⊥EF于点M,过E、F分别作∠MEP=∠MFP=30°就可以得到满足条件的点P,根据特殊直角三角形才求出PE,PF,PM,DP的长,进而得出答案.此题主要考查了解直角三角,正确画出图形进而求出PE的长是解题关键.

练习册系列答案
相关题目