题目内容
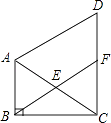
【题目】平行四边形ABCD的两个顶点A、C在反比例函数y= 
（k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，AD交y轴于P点 
（1）已知点A的坐标是（2，3），求k的值及C点的坐标；
（2）若△APO的面积为2，求点D到直线AC的距离．
【答案】
（1）解：∵点A的坐标是（2，3），平行四边形ABCD的两个顶点A、C在反比例函数y= 
（k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，
∴3= 
，点C与点A关于原点O对称，
∴k=6，C（﹣2，﹣3），
即k的值是6，C点的坐标是（﹣2，﹣3）
（2）解：∵△APO的面积为2，点A的坐标是（2，3），
∴ 
，得OP=2，
设过点P（0，2），点A（2，3）的直线解析式为y=ax+b，
解得， 
，
即直线PC的解析式为y= 
，
将y=0代入y= ，得x═﹣4，
∴OP=4，
∵A（2，3），C（﹣2，﹣3），
∴AC= 
，
设点D到AC的距离为m，
∵S△ACD=S△ODA+S△ODC，
∴ 
，
解得，m= 
，
即点D到直线AC的距离是
【解析】（1）根据点A的坐标是（2，3），平行四边形ABCD的两个顶点A、C在反比例函数y= （k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，可以求得k的值和点C的坐标；（2）根据△APO的面积为2，可以求得OP的长，从而可以求得点P的坐标，进而可以求得直线AP的解析式，从而可以求得点D的坐标，再根据等积法可以求得点D到直线AC的距离．本题考查反比例函数与一次函数的交点问题、平行四边形的性质，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)．
