题目内容
【题目】△ABC的内切圆的三个切点分别为D、E、F,∠A=75°,∠B=45°,则圆心角∠EOF=度. 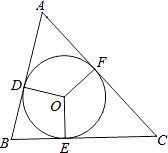
【答案】120
【解析】解:∵∠A=75°,∠B=45°,
∴∠C=180°﹣75°﹣45°
=105°﹣45°
=60°
∵△ABC的内切圆的三个切点分别为D、E、F,
∴∠OEC=∠OFC=90°,
∵四边形OECF的内角和等于360°,
∴∠EOF=360°﹣(90°+90°+60°)
=360°﹣240°
=120°
故答案为:120.
首先根据∠A=75°,∠B=45°,求出∠C=60°;然后根据△ABC的内切圆的三个切点分别为D、E、F,可得∠OEC=∠OFC=90°,再根据四边形OEFC的内角和等于360°,求出圆心角∠EOF的度数是多少即可.此题主要考查了三角形的内切圆与内心,要熟练掌握,解答此题的关键是要明确:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目