题目内容
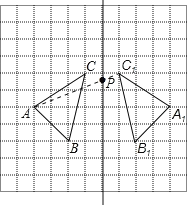
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

【答案】(1)作图见解析;(2)5;(3)点P即为所求的点.
【解析】试题分析:(1)根据轴对称性作△ABC中顶点A,B,C关于直线l的对称点A1,B1,C1,然后再连接A1,B1,C1可得△A1B1C1,(2)利用割补法求△ABC的面积,利用过△ABC各顶点的矩形减去三个直角三角形的面积可求解,(3)要在直线l要上找到一点P,使△PAC周长最短,因为AC长为定值,所以要使△PAC周长最短,则使PA+PC的和最短,可作C关于直线l的对称点C1,连接A C1, 则A C1与直线l的交点即为所求的点P.
试题解析:(1)所作图形如图所示,
(2) ![]() ,所以△ABC的面积为5,
,所以△ABC的面积为5,
(3)连接A C1,则A C1与直线l的交点P即为所求的点.

练习册系列答案
相关题目