题目内容
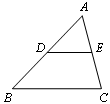
如图,△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③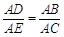 .④三角形ADE与梯形DECB的面积比为1:4,其中正确的有【 】
.④三角形ADE与梯形DECB的面积比为1:4,其中正确的有【 】
(A)3个 (B)2个 (C)1个 (D)0个
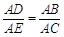 .④三角形ADE与梯形DECB的面积比为1:4,其中正确的有【 】
.④三角形ADE与梯形DECB的面积比为1:4,其中正确的有【 】
(A)3个 (B)2个 (C)1个 (D)0个
A
试题分析:由点D、E分别是AB、AC的中点根据三角形的中位线定理可得DE∥BC,BC=2DE,即可证得△ADE∽△ABC,再根据相似三角形的性质依次分析即可.
∵点D、E分别是AB、AC的中点
∴DE∥BC,BC=2DE
∴△ADE∽△ABC
∴
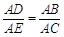 ,△ADE与△ABC的面积比为1:2
,△ADE与△ABC的面积比为1:2∴三角形ADE与梯形DECB的面积比为1:3
所以①、②、③正确,故选A.
点评:解题的关键是熟练掌握三角形的中位线平行于第三边,且等于第三边的一半;相似三角形的面积比等于相似比的平方.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
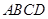 中,
中, 是边
是边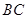 上的点,
上的点,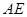 交
交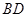 于点
于点 ,如果
,如果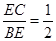 ,那么
,那么 的值为
的值为
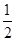
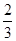



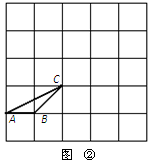

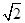 ∶1.
∶1.
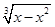 的值为( ).
的值为( ).