题目内容
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的坐标为
的坐标为![]() .点
.点![]() 是边
是边![]() 上的一个动点(不与
上的一个动点(不与![]() 重合),反比例函数
重合),反比例函数![]() 的图象经过点
的图象经过点![]() 且与边
且与边![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)当点![]() 是边
是边![]() 的中点时,求点
的中点时,求点![]() 坐标(用含
坐标(用含![]() 式子表示)
式子表示)
(2)在点![]() 的运动过程中,试证明:
的运动过程中,试证明:![]() 是一个定值.
是一个定值.
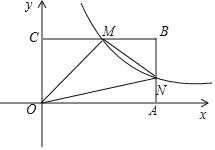
【答案】(1)N点的坐标是![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据待定系数法,可得反比例函数解析式,根据自变量与函数值的对应关系,可得答案;
(2)根据待定系数法,可得反比例函数解析式,根据自变量与函数值的对应关系,可得N点坐标,根据线段的和差,可得MB,BN,根据分式的性质,可得答案.
(1)矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,
得![]() .
.
反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
![]() ,
,
反比例函数![]() 的图象经过点
的图象经过点![]() 且与边
且与边![]() 交于点
交于点![]() ,
,
![]() 点的横坐标是
点的横坐标是![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点的坐标是
点的坐标是![]() .
.
(2)证明:设![]() 点坐标为
点坐标为![]() ,
,
![]() .
.
∵反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
![]() ,
,
∵反比例函数![]() 的图象经过点
的图象经过点![]() 且与边
且与边![]() 交于点
交于点![]() ,
,
![]() 点的横坐标是
点的横坐标是![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点的坐标是
点的坐标是![]() .
.
![]() ,
,
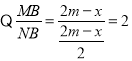 ,
,
![]() 是一个定值.
是一个定值.

【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?
【题目】今年“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数,单位:万人),已知9月30日的游客人数为0.3万人,请回答下列问题:
日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 | +1.8 | +0.8 | +0.2 | -0.4 | -0.8 | +0.2 | -1.0 |
(1)七天内游客人数最多的是 日,最少的是 日;
(2)若以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况?
(3)求这7天的游客人数是多少万人.