ЬтФПФкШн
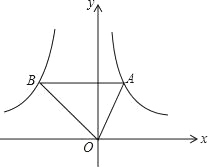
ЁОЬтФПЁПШчЭМЃЌЕуAЪЧЗДБШР§КЏЪ§y1=![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуAзї ABЁЮxжсЃЌНЛСэвЛИіБШР§КЏЪ§y2=
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуAзї ABЁЮxжсЃЌНЛСэвЛИіБШР§КЏЪ§y2=![]() ЃЈkЃМ0ЃЌxЃМ0ЃЉЕФЭМЯѓгкЕуBЃЎ
ЃЈkЃМ0ЃЌxЃМ0ЃЉЕФЭМЯѓгкЕуBЃЎ
ЃЈ1ЃЉШєSЁїAOBЕФУцЛ§ЕШгк3ЃЌдђkЪЧ=_____ЃЛ
ЃЈ2ЃЉЕБk=Љ8ЪБЃЌШєЕуAЕФКсзјБъЪЧ1ЃЌЧѓЁЯAOBЕФЖШЪ§ЃЛ
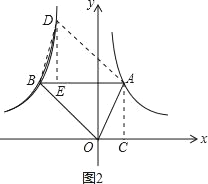
ЃЈ3ЃЉШєВЛТлЕуAдкКЮДІЃЌЗДБШР§КЏЪ§y2=![]() ЃЈkЃМ0ЃЌxЃМ0ЃЉЭМЯѓЩЯзмДцдквЛЕуDЃЌЪЙЕУЫФБпаЮAOBDЮЊЦНааЫФБпаЮЃЌЧѓkЕФжЕЃЎ
ЃЈkЃМ0ЃЌxЃМ0ЃЉЭМЯѓЩЯзмДцдквЛЕуDЃЌЪЙЕУЫФБпаЮAOBDЮЊЦНааЫФБпаЮЃЌЧѓkЕФжЕЃЎ
ЁОД№АИЁП(1)-4 (2) 90Ёу (3)-4
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУЗДБШР§КЏЪ§kгыУцЛ§ЕФЙиЯЕ.(2)РћгУABЦНааxжсЧѓГіBЕузјБъЃЌЧѓГіШ§БпЃЌдйЧѓЁЯAOB.(3) МйЩшy2=![]() ЩЯгавЛЕуDЃЌЪЙЫФБпаЮAOBDЮЊЦНааЫФБпаЮ,Й§DзїDEЁЭABЃЌЙ§AзїACЁЭxжс,жЄУї ЁїAOCЁеЁїDBE,ЧѓГіkжЕ.
ЩЯгавЛЕуDЃЌЪЙЫФБпаЮAOBDЮЊЦНааЫФБпаЮ,Й§DзїDEЁЭABЃЌЙ§AзїACЁЭxжс,жЄУї ЁїAOCЁеЁїDBE,ЧѓГіkжЕ.
ЪдЬтНтЮіЃК
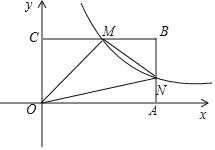
ЃЈ1ЃЉШчЭМ1ЃЌЩшABНЛyжсгкЕуCЃЌ
ЁпЕуAЪЧЗДБШР§КЏЪ§y1=![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФШЮвтвЛЕуЃЌЧвABЁЮxжсЃЌ
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФШЮвтвЛЕуЃЌЧвABЁЮxжсЃЌ
ЁрABЁЭyжсЃЌ
ЁрSЁїAOC=![]() ЁС2=1ЃЌ
ЁС2=1ЃЌ
ЁпSЁїAOB=3ЃЌ
ЁрSЁїBOC=2ЃЌ
Ёрk=Љ4ЃЛ

ЃЈ2ЃЉЁпЕуAЕФКсзјБъЪЧ1ЃЌ
Ёрy=2ЃЌ
ЁрЕуAЃЈ1ЃЌ2ЃЉЃЌ
ЁпABЁЮxжсЃЌ
ЁрЕуBЕФзнзјБъЮЊ2ЃЌ
Ёр2=Љ![]() ЃЌ
ЃЌ
НтЕУЃКx=Љ4ЃЌ
ЁрЕуBЃЈЉ4ЃЌ2ЃЉЃЌ
ЁрAB=AC+BC=1+4=5ЃЌOA=![]() ЃЌOB=2
ЃЌOB=2![]() ЃЌ
ЃЌ
ЁрOA2+OB2=AB2ЃЌ
ЁрЁЯAOB=90ЁуЃЛ
ЃЈ3ЃЉНтЃКМйЩшy2=![]() ЩЯгавЛЕуDЃЌЪЙЫФБпаЮAOBDЮЊЦНааЫФБпаЮЃЌ
ЩЯгавЛЕуDЃЌЪЙЫФБпаЮAOBDЮЊЦНааЫФБпаЮЃЌ
Й§DзїDEЁЭABЃЌЙ§AзїACЁЭxжсЃЌ
ЁпЫФБпаЮAOBDЮЊЦНааЫФБпаЮЃЌ
ЁрBD=OAЃЌBDЁЮOAЃЌ
ЁрЁЯDBA=ЁЯOAB=ЁЯAOCЃЌ
дкЁїAOCКЭЁїDBEжаЃЌ
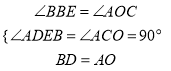 ,
,
ЁрЁїAOCЁеЁїDBEЃЈAASЃЉЃЌ
ЩшAЃЈaЃЌ ![]() ЃЉЃЈaЃО0ЃЉЃЌМДOC=aЃЌAC=
ЃЉЃЈaЃО0ЃЉЃЌМДOC=aЃЌAC=![]() ЃЌ
ЃЌ
ЁрBE=OC=aЃЌDE=AC=![]() ЃЌ
ЃЌ
ЁрDзнзјБъЮЊ![]() ЃЌBзнзјБъЮЊ
ЃЌBзнзјБъЮЊ![]() ЃЌ
ЃЌ
ЁрDКсзјБъЮЊ![]() ЃЌBКсзјБъЮЊ
ЃЌBКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЁрBE=|![]() Љ
Љ![]() |=aЃЌМДЉ
|=aЃЌМДЉ![]() =aЃЌ
=aЃЌ
Ёрk=Љ4ЃЎ