题目内容
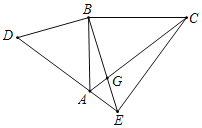
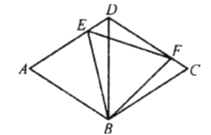
【题目】如图,菱形![]() 的边长为2,对角线
的边长为2,对角线![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的两个动点,且满足
上的两个动点,且满足![]() .
.
(1)求证: ![]() ;
;
(2)判断![]() 的形状,并说明理由,同时指出
的形状,并说明理由,同时指出![]() 是由
是由![]() 经过如何变换得到.
经过如何变换得到.
【答案】(1)证明见解析(2)等边三角形
【解析】试题分析:(1)先判定△ABD与△BCD都是等边三角形,根据等边三角形的性质可得∠BDE=∠C=60°,再求出DE=CF,然后利用“边边角”证明两三角形全等;
(2)根据全等三角形对应边相等可得BE=CF,全等三角形对应角相等可得∠DBE=∠CBF,然后求出∠EBF=60°,再根据等边三角形的判定得解,利用旋转变换解答.
试题解析:(1)证明:∵菱形ABCD的边长为2,对角线BD=2,∴AB=AD=BD=2,BC=CD=BD=2,∴△ABD与△BCD都是等边三角形,∴∠BDE=∠C=60°.∵AE+CF=2,∴CF=2﹣AE.又∵DE=AD﹣AE=2﹣AE,∴DE=CF.在△BDE和△BCF中,∵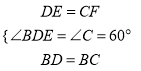 ,∴△BDE≌△BCF(SAS);
,∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,∴BE=BF,∠DBE=∠CBF,∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,∴△BEF是等边三角形,由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF.

练习册系列答案
相关题目