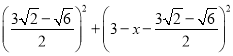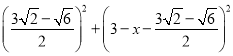题目内容
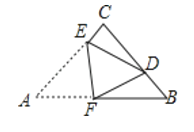
【题目】如图,将△ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
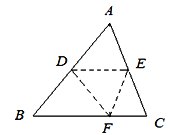
①△BDF是等腰三角形;
②DE=![]() BC;
BC;
③四边形ADFE是菱形;
④∠BDF+∠FEC=2∠A.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析:根据菱形的判定和等腰三角形的判定,采用排除法,逐条分析判断.
详解:∵三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,
∴AD=DF,AE=EF,∠ADE=∠B,∠ADE=∠EDF,∠EDF=∠DFB,
∴∠B=BFD,
∴△BDF是等腰三角形,故本选项①正确;
∴BD=DF,
∴AD=BD,同理可得出:AE=CE,
∴DE是△ABC的中位线,
∴![]() ;故本选项②正确;
;故本选项②正确;
∵AB不一定等于AC,
∴AD不一定等于EF,四边形ADFE不是平行四边形;
∴故本选项③错误;
∵△BDF是等腰三角形,∠B=∠BFD=∠ADE,
∴∠C=∠CFE=∠AED,
∴![]()
∴![]()
∴∠BDF+∠FEC=2∠A.
故本选项④正确.
故选C.

【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?