题目内容
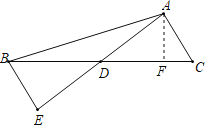
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.
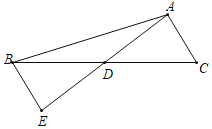
(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
【答案】(1)证明见解析;(2)90°;(3)![]() .
.
【解析】
(1)先证明△ADC≌△EDB,可得∠CAD=∠BED,进而可得结论;
(2)由勾股定理逆定理可得△ABE是直角三角形,∠E=90°,进而可得∠CAD=∠E=90°;
(3)先由勾股定理求CD,再由AFCD=ACAD可求AF即可.
解:(1)证明:∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,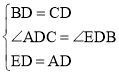 ,
,
∴△ADC≌△EDB(SAS),
∴∠CAD=∠BED,
∴BE∥AC.
(2)∵△ADC≌△EDB,
∴BE=AC=5,
在△ABE中,∵AB=13,BE=5,AE=2AD=12,
∴AE2+BE2=122+52=169,AB2=132=169,
∴AE2+BE2=AB2
∴∠E=90°,
∵BE∥AC,
∴∠CAD=∠E=90°;
(3)如图,过点A作AF⊥BC于F,
在Rt△ACD中,CD=![]() =
=![]() =
=![]() ,
,
∵AFCD=ACAD,
∴AF=![]() =
=![]() =
=![]() ,
,
即点A到BC的距离为![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
【题目】观察下列图形,它是把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,将这种做法继续下去(如图2,图3…).观察规律解答以下各题:
 ……
……
(1)填写下表:
图形序号 | 挖去三角形的个数 |
图1 | 1 |
图2 | 1+3 |
图3 | 1+3+9 |
图4 |
(2)根据这个规律,求图n中挖去三角形的个数fn(用含n的代数式表示);
(3)若图n+1中挖去三角形的个数为fn+1,求fn+1-fn