题目内容
21、已知：△ABC中，D是BC上的一点，E、F、G、H分别是BD、BC、AC、AD的中点，求证：EG、HF互相平分．
分析：根据三角形的中位线定理可判定四边形EHGF为平行四边形，根据平行四边形的性质即可得到EG、HF互相平分．
解答：
证明：连接EH，GH，GF，
∵E、F、G、H分别是BD、BC、AC、AD的中点，
∴AB∥EH∥GF，GH∥BC∥BF．
∴四边形EHGF为平行四边形．
∵GE，HF分别为其对角线，
∴EG、HF互相平分．
证明：连接EH，GH，GF，∵E、F、G、H分别是BD、BC、AC、AD的中点，
∴AB∥EH∥GF，GH∥BC∥BF．
∴四边形EHGF为平行四边形．
∵GE，HF分别为其对角线，
∴EG、HF互相平分．
点评：此题主要考查学生对三角形中位线定理及平行四边形的判定及性质的综合运用．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
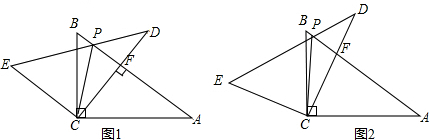
如图所示，已知在△ABC中，AB=AC，∠BAD=β，且AD=AE，求∠EDC．（用β表示）
8、如图，已知在△ABC中，AD垂直平分BC，AC=EC，点B、D、C、E在同一直线上，则下列结论：①AB=AC；②∠CAE=∠E；③AB+BD=DE；④∠BAC=∠ACB．正确的个数有（ ）个．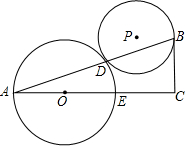
外切于点D，若AC和BC边的长是关于x的方程x2-（AB+4）x+4AB+8=0的两根，且25BC•sinA=9AB，