题目内容
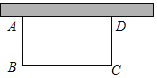
【题目】如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长24m.设AB长为x m,矩形的面积为S m2.
(1)写出S与x的函数关系式;
(2)当AB长为多少米时,所围成的花圃面积最大?最大值是多少?
(3)当花圃的面积为150m2时,AB长为多少米?
【答案】(1)S=﹣2x2+40x;(2)当x=10时,所围成的花圃面积最大,最大值为200m2;(3)当花圃的面积为150m2时,AB长为15米.
【解析】
(1)由AB=CD=x知BC=40﹣2x,根据矩形的面积公式可得函数解析式;
(2)将所得函数解析式配方成顶点式后,利用二次函数的性质求解可得;
(3)在函数解析式中令y=150,求出x的值,再由x的范围取舍即可得.
解:(1)S=x(40﹣2x)=﹣2x2+40x,
即函数关系式为:S=﹣2x2+40x;
(2)由题意,得:0<40﹣2x≤24,
解得8≤x<20,
又由(1),得S=﹣2(x﹣10)2+200,
∴当x=10时,所围成的花圃面积最大,最大值为200m2;
(3)由﹣2(x﹣10)2+200=150,
解得 x1=5,x2=15,
∵8≤x<20,
∴当花圃的面积为150m2时,AB长为15米.

练习册系列答案
相关题目