Question

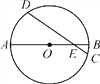
【题目】如图，⊙O的直径AB与弦CD相交于点E，若AE＝5，BE＝1，CD＝4，则∠AED＝____．

Answer 1

【答案】30°

【解析】试题分析：连接OD，过圆心O作OH⊥CD于点H．根据垂径定理求得DH=CH=；然后根据已知条件“AE=5，BE=1”求得⊙O的直径AB=6，从而知⊙O的半径OD=3，OE=2；最后利用勾股定理求得OH=1，再由30°角所对的直角边是斜边的一半来求∠AED．解：连接OD，过圆心O作OH⊥CD于点H．∴DH=CH=又∵AE=5，BE=1，∴AB=6，∴OA=OD=3（⊙O的半径）；∴OE=2；∴在Rt△ODH中，OH=1（勾股定理）；在Rt△OEH中，OH=∴∠OEH=30°，即∠AED=30°．故答案是：30°．