题目内容
【题目】综合题
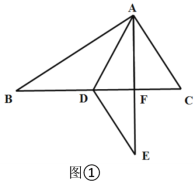
(1)如图1,AC和BD相交于点O,OA=OC,OB=OD,求证:DC∥AB.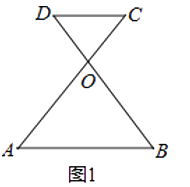
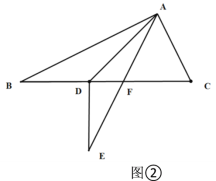
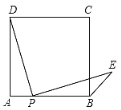
(2)如图2,在⊙O中,直径AB=6,AB与弦CD相交于点E,连接AC、BD,若AC=2,求cosD的值.
【答案】
(1)证明:在△AOB和△COD中,
 ,
,
∴△AOB≌△COD,
∴∠A=∠ACD,
∴DC∥AB
(2)解:连接BC,

∵AB为直径,
∴∠ACB=90°,
∴cosA= ![]() =
= ![]() ,
,
由圆周角定理得,∠D=∠A,
∴cosD= ![]() .
.
【解析】(1)根据全等三角形的判定方法(SAS)得到△AOB≌△COD,再根据全等三角形对应角相等,得到内错角∠A=∠ACD,根据内错角相等两直线平行,得出结论.(2)根据直径所对的圆周角是直角得到直角三角形,再根据圆周角定理得到∠D=∠A,得到cosA=cosD.
【考点精析】本题主要考查了垂径定理和解直角三角形的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目