ЬтФПФкШн
ЁОЬтФПЁПШчЭМ,дкЁїABCжа.AC=BC=5.AB=6.CDЪЧABБпжаЯп.ЕуPДгЕуCГіЗЂЃЌвдУПУы2.5ИіЕЅЮЛГЄЖШЕФЫйЖШбиC-D-CдЫЖЏ.дкЕуPГіЗЂЕФЭЌЪБЃЌЕуQвВДгЕуCГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиБпCAЯђЕуAдЫЖЏ.ЕБвЛИіЕуЭЃжЙдЫЖЏЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtУы.
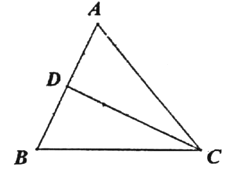
ЃЈ1ЃЉгУКЌtЕФДњЪ§ЪНБэЪОCPЁЂCQЕФГЄЖШ.
ЃЈ2ЃЉгУКЌtЕФДњЪ§ЪНБэЪОЁїCPQЕФУцЛ§.
ЃЈ3ЃЉЕБЁїCPQгыЁїCADЯрЫЦЪБЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉЕБ0ЃМtЁм![]() ЪБЃЌCP=2.5tЃЌCQ=2tЃЛЕБ
ЪБЃЌCP=2.5tЃЌCQ=2tЃЛЕБ![]() ЪБЃЌCP=8-2.5tЃЌCQ=2tЃЎ
ЪБЃЌCP=8-2.5tЃЌCQ=2tЃЎ
ЃЈ2ЃЉЕБ0ЃМtЁм![]() ЪБЃЌSЁїCPQ=
ЪБЃЌSЁїCPQ=![]() PCsinЁЯACDCQ=
PCsinЁЯACDCQ=![]() ЁС2.5tЁС
ЁС2.5tЁС![]() ЁС2t=
ЁС2t=![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌSЁїCPQ=
ЪБЃЌSЁїCPQ=![]() PCsinЁЯACDCQ=
PCsinЁЯACDCQ=![]() ЁСЃЈ8-2.5tЃЉЁС
ЁСЃЈ8-2.5tЃЉЁС![]() ЁС2t=
ЁС2t=![]() .
.
ЃЈ3ЃЉ0ЃМtЁм![]() Лђ
Лђ![]() s
s
ЁОНтЮіЁП
ЃЈ1ЃЉЗжСНжжЧщаЮЃКЕБ0ЃМtЁм![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЃМt
ЃМt![]() ЪБЃЌЗжБ№ЧѓНтМДПЩЃЎ
ЪБЃЌЗжБ№ЧѓНтМДПЩЃЎ
ЃЈ2ЃЉЗжСНжжЧщаЮЃКЕБ0ЃМtЁм![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЃМtЁм
ЃМtЁм![]() ЪБЃЌИљОнSЁїCPQ=
ЪБЃЌИљОнSЁїCPQ=![]() PCsinЁЯACDCQЗжБ№ЧѓНтМДПЩЃЎ
PCsinЁЯACDCQЗжБ№ЧѓНтМДПЩЃЎ
ЃЈ3ЃЉЗжСНжжЧщаЮЃКЕБ0ЃМtЁм![]() ЃЌПЩвджЄУїЁїQCPЁзЁїDCAЃЌЕБ
ЃЌПЩвджЄУїЁїQCPЁзЁїDCAЃЌЕБ![]() ЃМt
ЃМt![]() ЃЌЁЯQPC=90ЁуЪБЃЌЁїQPCЁзЁїADCЃЌЙЙНЈЗНГЬЧѓНтМДПЩЃЎ
ЃЌЁЯQPC=90ЁуЪБЃЌЁїQPCЁзЁїADCЃЌЙЙНЈЗНГЬЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпCA=CBЃЌAD=BD=3ЃЌ
ЁрCDЁЭABЃЌ
ЁрЁЯADC=90ЁуЃЌ
ЁрCD=![]() =
=![]() =4ЃЌ
=4ЃЌ
ЕБ0ЃМtЁм![]() ЪБЃЌCP=2.5tЃЌCQ=2tЃЌ
ЪБЃЌCP=2.5tЃЌCQ=2tЃЌ
ЕБ![]() ЪБЃЌCP=8-2.5tЃЌCQ=2tЃЎ
ЪБЃЌCP=8-2.5tЃЌCQ=2tЃЎ
ЃЈ2ЃЉЁпsinЁЯACD=![]() =
=![]() ЃЌ
ЃЌ
ЁрЕБ0ЃМtЁм![]() ЪБЃЌSЁїCPQ=
ЪБЃЌSЁїCPQ=![]() PCsinЁЯACDCQ=
PCsinЁЯACDCQ=![]() ЁС2.5tЁС
ЁС2.5tЁС![]() ЁС2t=
ЁС2t=![]()
ЕБ![]() ЪБЃЌSЁїCPQ=
ЪБЃЌSЁїCPQ=![]() PCsinЁЯACDCQ=
PCsinЁЯACDCQ=![]() ЁСЃЈ8-2.5tЃЉЁС
ЁСЃЈ8-2.5tЃЉЁС![]() ЁС2t=
ЁС2t=![]() .
.
ЃЈ3ЃЉЂйЕБ0ЃМtЁм![]() ЪБЃЌ
ЪБЃЌ
ЁпCP=2.5tЃЌCQ=2tЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
Ёп![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯPCQ=ЁЯACDЃЌ
Ёр0ЃМtЁм![]() ЪБЃЌЁїQCPЁзЁїDCAЃЌ
ЪБЃЌЁїQCPЁзЁїDCAЃЌ
ЂкЕБ![]() ЪБЃЌЕБЁЯQPC=90ЁуЪБЃЌЁїQPCЁзЁїADCЃЌ
ЪБЃЌЕБЁЯQPC=90ЁуЪБЃЌЁїQPCЁзЁїADCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФtЕФжЕЮЊЃК0ЃМtЁм![]() Лђ
Лђ![]() sЪБЃЌЁїQCPЁзЁїDCAЃЎ
sЪБЃЌЁїQCPЁзЁїDCAЃЎ

ЁОЬтФПЁПФГХњВЪЩЋЕЏСІЧђЕФжЪСПМьбщНсЙћШчЯТБэЃК
ГщШЁЕФВЪЩЋЕЏСІЧђЪ§n | 500 | 1000 | 1500 | 2000 | 2500 |
гХЕШЦЗЦЕЪ§m | 471 | 946 | 1426 | 1898 | 2370 |
гХЕШЦЗЦЕТЪ | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
ЃЈ1ЃЉЧыдкЭМжаЭъГЩетХњВЪЩЋЕЏСІЧђЁАгХЕШЦЗЁБЦЕТЪЕФелЯпЭГМЦЭМ
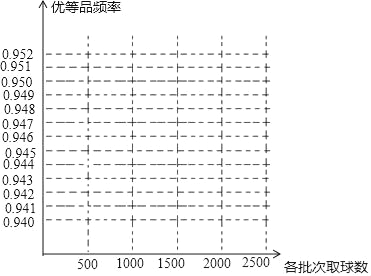
ЃЈ2ЃЉетХњВЪЩЋЕЏСІЧђЁАгХЕШЦЗЁБИХТЪЕФЙРМЦжЕДѓдМЪЧЖрЩйЃПЃЈОЋШЗЕН0.01ЃЉ
ЃЈ3ЃЉДгетХњВЪЩЋЕЏСІЧђжабЁдё5ИіЛЦЧђЁЂ13ИіКкЧђЁЂ22ИіКьЧђЃЌЫќУЧГ§СЫбеЩЋЭтЖМЯрЭЌЃЌНЋЫќУЧЗХШывЛИіВЛЭИУїЕФДќзгжаЃЌЧѓДгДќзгжаУўГівЛИіЧђЪЧЛЦЧђЕФИХТЪЃЎ
ЃЈ4ЃЉЯжДгЕкЃЈ3ЃЉЮЪЫљЫЕЕФДќзгжаШЁГіШєИЩИіКкЧђЃЌВЂЗХШыЯрЭЌЪ§СПЕФЛЦЧђЃЌНСАшОљдШЃЌЪЙДгДќзгжаУўГівЛИіЛЦЧђЕФИХТЪЮЊ![]() ЃЌЧѓШЁГіСЫЖрЩйИіКкЧђЃП
ЃЌЧѓШЁГіСЫЖрЩйИіКкЧђЃП




