ЬтФПФкШн
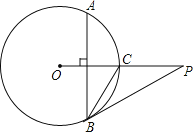
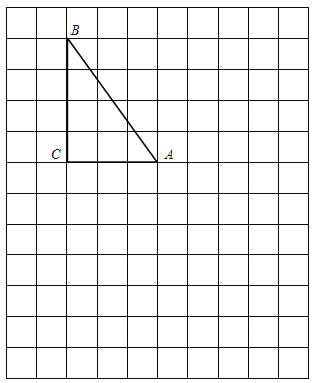
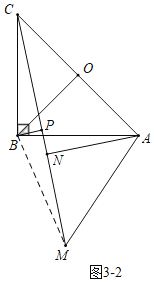
ЁОЬтФПЁПвбжЊЃЌдкЁїABCжаЃЌЁЯABCЃН90ЁуЃЌABЃНBCЃН4ЃЌЕуOЪЧБпACЕФжаЕуЃЌСЌНгOBЃЌНЋЁїAOBШЦЕуAЫГЪБеыа§зЊІСЁужСЁїANMЃЌСЌНгCMЃЌЕуPЪЧЯпЖЮCMЕФжаЕуЃЌСЌНгPBЃЌPNЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБІСЃН180ЪБЃЌЧыжБНгаДГіЯпЖЮPNКЭPBжЎМфТњзуЕФЮЛжУКЭЪ§СПЙиЯЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ0ЃМІСЃМ180ЪБЃЌЧыЬНЫїЯпЖЮPNКЭPBжЎМфТњзуКЮЮЛжУКЭЪ§СПЙиЯЕЃПжЄУїФуЕФНсТл
ЃЈ3ЃЉЕБЁїAOBа§зЊжСCЃЌMЃЌNШ§ЕуЙВЯпЪБЃЌЯпЖЮBPЕФГЄЮЊЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉPBЃНPNЃЌPBЁЭPNЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉPBЃНPNЃЌPBЁЭPNЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]() ЁР
ЁР![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌНсТлЃКPBЃНPNЃЌPBЁЭPNЃЎРћгУжБНЧШ§НЧаЮаББпЕФжаЯпЕФаджЪвдМАдВжмНЧЖЈРэНтОіЮЪЬтМДПЩЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌНсТлЃКPBЃНPNЃЌPBЁЭPNЃЎбгГЄBPЕНGЃЌЪЙЕУPGЃНPBЃЌСЌНгGMЃЌGNЃЌBNЃЎЯыАьЗЈжЄУїЁїBNGЪЧЕШбќжБНЧШ§НЧаЮМДПЩЃЎ
ЃЈ3ЃЉЗжСНжжЧщаЮЃКЂйШчЭМ3Љ1жаЃЌСЌНгBMЃЎжЄУїЁїABMЪЧЕШБпШ§НЧаЮЃЌBPЁЭCMМДПЩНтОіЮЪЬтЃЎ
ЂкШчЭМ3Љ2жаЃЌЕБCЃЌNЃЌMЙВЯпЪБЃЌЗНЗЈРрЫЦЂйЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌНсТлЃКPBЃНPNЃЌPBЁЭPNЃЎ
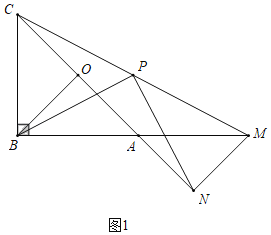
РэгЩЃКЕБІСЃН180ЁуЪБЃЌCЃЌAЃЌNЙВЯпЃЌBЃЌAЃЌMЙВЯпЃЌ
ЁпЁЯCNMЃНЁЯCBMЃН90ЁуЃЌPCЃНPMЃЌ
ЁрPBЃНPCЃНPMЃНPNЃЌ
ЁрCЃЌBЃЌNЃЌMЫФЕуЙВдВЃЌ
ЁрЁЯBPNЃН2ЁЯBMNЃЌ
ЁпЁЯAMNЃН45ЁуЃЌ
ЁрЁЯBPNЃН90ЁуЃЌ
ЁрPBЃНPNЃЌPBЁЭPNЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌНсТлЃКPBЃНPNЃЌPBЁЭPNЃЎ
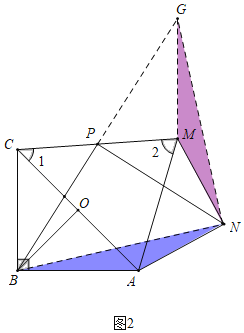
РэгЩЃКбгГЄBPЕНGЃЌЪЙЕУPGЃНPBЃЌСЌНгGMЃЌGNЃЌBNЃЎ
ЁпPCЃНPMЃЌЁЯCPBЃНЁЯMPGЃЌPBЃНPGЃЌ
ЁрЁїCPBЁеЁїMPGЃЈSASЃЉЃЌ
ЁрBCЃНGMЃНABЃЌЁЯBCPЃНЁЯGMPЃНЁЯ1+45ЁуЃЌ
ЁрЁЯGMNЃН360ЁуЉЁЯGMPЉЁЯ2ЉЁЯAMNЃН360ЁуЉЁЯ1Љ45ЁуЉЁЯ2Љ45ЁуЃН270ЁуЉЁЯ1ЉЁЯ2ЃЌ
ЁпЁЯBANЃН45Ёу+ЁЯCAM+45ЁуЃН90Ёу+ЃЈ180ЁуЉЁЯ1ЉЁЯ2ЃЉЃН270ЁуЉЁЯ1ЉЁЯ2ЃЌ
ЁрЁЯNMGЃНЁЯBANЃЌ
ЁрABЃНMGЃЌANЃНNMЃЌ
ЁрЁїBANЁеЁїGMNЃЈSASЃЉЃЌ
ЁрBNЃНGNЃЌЁЯBNAЃНЁЯGNMЃЌ
ЁрЁЯBNGЃНЁЯANMЃН90ЁуЃЌ
ЁпPBЃНPGЃЌ
ЁрPNЃНPBЃНPGЃЌPNЁЭBGЃЌ
МДPBЃНPNЃЌPNЁЭPBЃЎ
ЃЈ3ЃЉЂйШчЭМ3Љ1жаЃЌСЌНгBMЃЎ
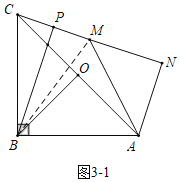
ЕБCЃЌMЃЌNЙВЯпЪБЃЌЁпЁЯCNAЃН90ЁуЃЌACЃН2ANЃЌ
ЁрЁЯACNЃН30ЁуЃЌ
ЁпЁЯNMAЃНЁЯMCA+ЁЯMACЃН45ЁуЃЌ
ЁрЁЯCAMЃН15ЁуЃЌ
ЁпЁЯMABЃНЁЯVAM+ЁЯOABЃН60ЁуЃЌ
ЁпABЃНAMЃЌ
ЁрЁїABMЪЧЕШБпШ§НЧаЮЃЌ
ЁрBAЃНBMЃНBCЃЌ
ЁпPCЃНPMЃЌ
ЁрBPЁЭCMЃЌ
ЁпABЃНBCЃН4ЃЌ
ЁрACЃН4![]() ЃЌ
ЃЌ
ЁрANЃНOAЃН2![]() ЃЌCNЃН
ЃЌCNЃН![]() ANЃН2
ANЃН2![]() ЃЌ
ЃЌ
ЁрCMЃНCNЉMNЃН2![]() Љ2
Љ2![]() ЃЌ
ЃЌ
ЁрPCЃН![]() Љ
Љ![]() ЃЌ
ЃЌ
ЁрPBЃН![]() ЃЎ
ЃЎ
ЂкШчЭМ3Љ2жаЃЌЕБCЃЌNЃЌMЙВЯпЪБЃЌЭЌЗЈПЩжЄЁЯACNЃН30ЁуЃЌЁЯBANЃН15ЁуЃЌЁЯBAMЃН60ЁуЃЌ
ЁрЁїABMЪЧЕШБпШ§НЧаЮЃЌ
ЁрBMЃНBAЃНBCЃЌ
ЁпPCЃНPMЃЌ
ЁрBPЁЭCMЃЌ
ЁрPBЃН![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФBPЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ![]() ЃЎ
ЃЎ

ЁОЬтФПЁПАЫЃЈ2ЃЉАрзщжЏСЫвЛДЮОЕфЫаЖСБШШќЃЌМзЁЂввСНЖгИї10ШЫЕФБШШќГЩМЈШчЯТБэЃЈ10ЗжжЦЃЉЃК
Мз | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
вв | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
ЃЈ1ЃЉМзЖгГЩМЈЕФжаЮЛЪ§ЪЧЁЁ ЁЁЗжЃЌввЖгГЩМЈЕФжкЪ§ЪЧЁЁ ЁЁЗжЃЛ
ЃЈ2ЃЉМЦЫуввЖгЕФЦНОљГЩМЈКЭЗНВюЃЛ
ЃЈ3ЃЉвбжЊМзЖгГЩМЈЕФЗНВюЪЧ1.4ЃЌдђГЩМЈНЯЮЊећЦыЕФЪЧЁЁ ЁЁЖгЃЎ