题目内容
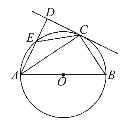
【题目】如图,已知AB是☉O的直径,DC是☉O的切线,点C是切点,AD⊥DC,垂足为D,且与圆O相交于点E.
(1)求证:∠DAC=∠BAC.
(2)若☉O的直径为5cm,EC=3cm,求AC的长.
【答案】(1)证明见解析;(2)4.
【解析】
(1)连接OC,推出OC⊥DC,求出AD∥OC,得出∠DAC=∠BAC=∠OCA,即可得出答案;
(2)根据∠DAC=∠BAC推出EC=BC=3,在△ACB中根据勾股定理求出AC即可.
(1)证明:连接OC,
∵DC切O于C,
∴OC⊥DC,
∵AD⊥DC,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠DAC=∠BAC.

(2)∵∠DAC=∠BAC,
∴EC=BC=3,
∵AB是直径,
∴∠ACB=90°,
由勾股定理得:![]()
答:AC的长是4.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目