题目内容
【题目】定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．
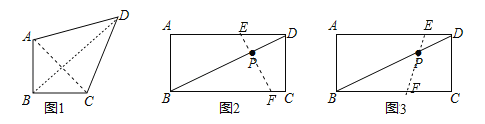
（1）如图1，等腰直角四边形ABCD，AB=BC，∠ABC=90°．
①若AB=CD=1，AB∥CD，求对角线BD的长．
②若AC⊥BD，求证：AD=CD；
（2）如图2，在矩形ABCD中，AB=5，BC=9，点P是对角线BD上一点，且BP=2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形，求AE的长．
【答案】（1）①
；②证明见解析；（2）5或6.5．
【解析】
试题分析：（1）①只要证明四边形ABCD是正方形即可解决问题；
②只要证明△ABD≌△CBD，即可解决问题；
（2）若EF⊥BC，则AE≠EF，BF≠EF，推出四边形ABFE表示等腰直角四边形，不符合条件．若EF与BC不垂直，①当AE=AB时，如图2中，此时四边形ABFE是等腰直角四边形，②当BF=AB时，如图3中，此时四边形ABFE是等腰直角四边形，分别求解即可；
试题解析：（1）①∵AB=AC=1，AB∥CD，∴S四边形ABCD是平行四边形，∵AB=BC，∴四边形ABCD是菱形，∵∠ABC=90°，∴四边形ABCD是正方形，∴BD=AC=
=．
（2）如图1中，连接AC、BD．
∵AB=BC，AC⊥BD，∴∠ABD=∠CBD，∵BD=BD，∴△ABD≌△CBD，∴AD=CD．
（2）若EF⊥BC，则AE≠EF，BF≠EF，∴四边形ABFE表示等腰直角四边形，不符合条件．
若EF与BC不垂直，①当AE=AB时，如图2中，此时四边形ABFE是等腰直角四边形，∴AE=AB=5．
②当BF=AB时，如图3中，此时四边形ABFE是等腰直角四边形，∴BF=AB=5，∵DE∥BF，∴BF=PB=1：2，∴DE=2.5，∴AE=9﹣2.5=6.5，综上所述，满足条件的AE的长为5或6.5．
