题目内容
【题目】给出下列命题：①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；②三角形的三边a、b、c满足a2+c2＝b2，则∠C＝90°；③△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形；④△ABC中，若a：b：c＝1：2：
，则这个三角形是直角三角形，其中，正确命题为_____（选填序号）．
【答案】③④
【解析】
根据勾股定理、三角形内角和定理、勾股定理的逆定理判断．
解：①在直角三角形
中，已知两边长为3和4，
当4是直角边时，第三边
，
当4是斜边长时，第三边
则第三边长为5或
，本说法是假命题；
②三角形的三边
、
、
满足
，则
，本说法是假命题；
③
中，若
，
设
、
、
分别为
、
、
，
则
，
解得，
，
则、、分别为
、
、
，
则是直角三角形，本说法是真命题；
④中，若
，
设、、分别为、
、
，
，
，
，
这个三角形是直角三角形，本说法是真命题，
故答案为：③④．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
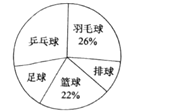
【题目】某中学为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1500名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称 | 人数 |
乒乓球 | 42 |
羽毛球 | a |
排球 | 15 |
篮球 | 33 |
足球 | b |
解答下列问题：
（1）这次抽样调查中的样本是________；
（2）统计表中，a=________，b=________；
（3）试估计上述1500名学生中最喜欢乒乓球运动的人数.
