题目内容
【题目】如图，AC是□ABCD的一条对角线，过AC中点O的直线分别交AD，BC于点E，F．
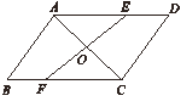
（1）求证：△AOE≌△COF；
（2）若EF与AC垂直，试判断四边形AFCE的形状，并说明理由．
【答案】（1）详见解析；（2）四边形AFCE是菱形，理由详见解析．
【解析】
（1）由平行四边形的性质得出AD∥BC，得出∠EAO=∠FCO，利用对顶角相等∠AOE=∠COF，O是AC的中点，OA=OC，所以由ASA即可得出结论；（2）四边形AFCE是菱形，先证明四边形AFCE是平行四边形，再由对角线互相垂直的平行四边形是菱形即可得出四边形AFCE是菱形．
（1）∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EAO=∠FCO，
∵O是CA的中点
∴OA=OC，
又∵∠AOE=∠COF（对顶角相等），
∴△AOE≌△COF（ASA）；
（2）四边形AFCE是菱形，理由如下：
∵△AOE≌△COF，
∴AE=CF，
∵AE∥CF，
∴四边形AFCE是平行四边形（一组对边平行且相等的四边形是平行四边形），
∵EF⊥AC，
∴四边形AFCE是菱形（对角线互相垂直的平行四边形是菱形）．
练习册系列答案
相关题目
【题目】某中学为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1500名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称 | 人数 |
乒乓球 | 42 |
羽毛球 | a |
排球 | 15 |
篮球 | 33 |
足球 | b |
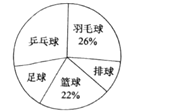
解答下列问题：
（1）这次抽样调查中的样本是________；
（2）统计表中，a=________，b=________；
（3）试估计上述1500名学生中最喜欢乒乓球运动的人数.
