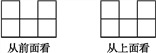
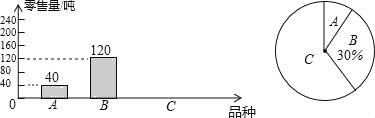
题目内容
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8 cm,BD=2 cm.
(1)图中共有多少条线段?
(2)求AC的长.
(3)若点E在直线AD上,且EA=3 cm,求BE的长.
![]()
【答案】(1)6;(2)4cm;(3)9cm或3cm.
【解析】试题分析:(1)根据线段的定义找出图中所有线段,图中线段有:AC,AB,AD,CB,CD,BD共6条,
(2)根据线段的和差关系和线段中点性质进行计算可得: AC= AD-CD= AD-2BD=8-4=4,
(3)因为点E在直线AD上,且EA=3cm,题目中没有明确点E 的具体位置,所以要分两种情况讨论, ①点E在A点的左侧时, ②点E在A点的右侧时,利用线段和差关系分别进行计算.
试题解析:(1)图中共有6条线段,
(2)∵点B为CD的中点,
∴CD=2BD,
∵BD=2 cm,
∴CD=4 cm,
∵AC=AD-CD且AD=8 cm,CD=4 cm,
∴AC=4 cm,
(3)当E在点A的左边时,则BE=BA+EA且BA=6 cm,EA=3 cm,
∴BE=9 cm.
当E在点A的右边时,则BE=AB-EA且AB=6 cm,EA=3 cm,
∴BE=3 cm.
∴BE=9 cm或BE=3 cm.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目