Question

【题目】已知,如图,在矩形ABCD中,AB=4,BC=6,点E为线段AB上一动点(不与点A. 点B重合)，先将矩形ABCD沿CE折叠，使点B落在点F处，CF交AD于点H.

(1)求证：△AEG∽△DHC；

(2)若折叠过程中，CF与AD的交点H恰好是AD的中点时，求tan∠BEC的值；

(3)若折叠后，点B的对应F落在矩形ABCD的对称轴上，求此时AE的长.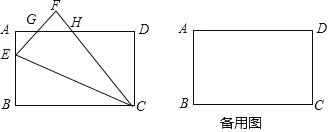

Answer 1

【答案】（1）见解析；（2）3 （3）或.

【解析】

（1）根据矩形的性质得到CD=AB=4，AD=BC=6，∠A=∠B=∠D=90°，根据折叠的性质得到∠F=∠B=90°，根据余角的性质得到∠AEG=∠DHC，于是得到结论；

（2）由点H是AD的中点，得到AH=DH=3，根据相似三角形的性质得到GH=，得到AG=AD-GH-DH=，BE=2，根据三角函数的定义即可得到结论；

（3）分两种情况考虑：F在横对称轴上与F在竖对称轴上，分别求出BF的长即可．

(1)∵在矩形ABCD中，AB=4，BC=6，

∴CD=AB=4,AD=BC=6,∠A=∠B=∠D=90°，

∵将矩形ABCD沿CE折叠，使点B落在点F处，

∴∠F=∠B=90°，

∵∠AGE=∠FGH，∠FHG=∠DHC，

∵∠FGH+∠FHG=90°，

∴∠AGE+∠DHC=90°，

∵∠AEG+∠AGE=90°，

∴∠AEG=∠DHC，

∴△AEG∽△DHC；

(2)∵点H是AD的中点，

∴AH=DH=3，

∵CD=4，

∴CH=5，FH=1，

∵∠F=∠D=90°，∠FHG=∠DHC，

∴△FHG∽△DHC，

∴，

∴GH=，

∴AG=ADGHDH=，

∵△AEG∽△DHC，

∴，

∴AE=1，

∴BE=2，

∴tan∠BEC==3,

(3)当F在横对称轴MN上,如图2所示,此时CN=CD=2，CF=BC=6，

∴FN=，

∴MF=，

由折叠得，EF=BE，EM=2BE，

∴，

即，

∴BE=，

∴AE=

当F在竖对称轴MN上时,如图3所示,此时AB∥MN∥CD，

∴∠BEC=∠FOE，

∵∠BEC=∠FEC，

∴∠FEC=∠FOE，

∴EF=OF，

由折叠的性质得,BE=EF,∠EFC=∠B=90°，

∵BN=CN，

∴OC=OE，

∴FO=OE，

∴△EFO是等边三角形，

∴∠FEC=60°，

∴∠BEC=60°，

∴BE=BC=，

∴AE=.

综上所述,点B的对应F落在矩形ABCD的对称轴上,此时AE的长是或.