题目内容
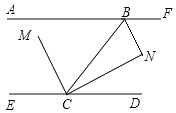
【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

【答案】(1)∠DCN=30°;(2)见解析
【解析】
(1)先根据平行线性质求出∠BCE和∠BCD,再根据角平分线的性质求出∠MCB,然后根据角的和差可得∠BCN,继而可得答案;
(2)先求出∠FBC和∠NBC,然后根据平行线的判定方法即可证得结论.
解:(1)∵AF∥DE,∠ABC=60°,
∴∠BCE=180°﹣60°=120°,∠BCD=∠ABC=60°,
∵CM平分∠BCE,
∴∠MCB=60°,
∵∠MCN=90°,
∴∠BCN=90°﹣60°=30°,
∴∠DCN=60°﹣30°=30°;
(2)∵∠ABC=60°,
∴∠FBC=120°,
∵BN平分∠FBC,
∴∠NBC=60°,
∵∠BCM=60°,
∴∠NBC=∠BCM,
∴BN∥CM.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目