Question

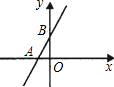已知n为正整数，一次函数y=

n+1

n

x+n+l的图象与坐标轴围成三角形的外接圆面积为π，求此一次函数的解析式．

Answer 1

分析：分别令x=0，y=0求出y轴、x轴的交点坐标，再求出△ABO外接圆的面积，再根据勾股定理即可求出n的值，进而可求出此一次函数的解析式．

解答：解：当y=0时，得x=-a，
∴直线与x轴交点为（-n，0），
当x=0时，得y=n+1，
∴直线与y轴的交点为B（0，n+1），
∵Rt△ABO的外接圆面积S=（

|AB|

2

）²π=π，
∴|AB|=2，
由|AO|²+|BO|²=|AB|²，得n²+（n+1）²=2，即n²+n-12=0，
∴n=3，
∴一次函数的解析式为y=

4

3

x+4．
故答案为：y=

4

3

x+4．

点评：本题考查的是一次函数综合题，涉及到三角形的外接圆、直线与坐标轴的交点、勾股定理等相关知识．