题目内容
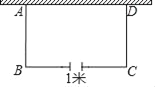
【题目】某农场准备围建一个矩形养鸡场,其中一边靠墙(墙的长度为15米),其余部分用篱笆围成,在墙所对的边留一道1米宽的门,已知篱笆的总长度为23米.
(1)设图中AB(与墙垂直的边)长为x米,则AD的长为 米(请用含x的代数式表示);
(2)若整个鸡场的总面积为y米2,求y的最大值.
【答案】(1)24﹣2x;(2)y的最大值为72米2.
【解析】
(1)根据题意列代数式即可得到结论;
(2)根据题意列出函数关系式,然后,根据二次函数的性质即可得到结论.
解:(1)由题意得,AD=23+1﹣2x=24﹣2x,
故答案为:24﹣2x;
(2)根据题意得,y=x(24﹣2x)=﹣2x2+24x=﹣2(x﹣6)2+72,
∴y的最大值为72米2.

练习册系列答案
相关题目