题目内容
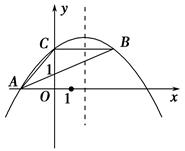
在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).
(1)当k=-2时,求反比例函数的解析式;
(2)要使反比例函数与二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围.
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(1)当k=-2时,求反比例函数的解析式;
(2)要使反比例函数与二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围.
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(1)y=-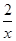 (2)k<0 x≤-
(2)k<0 x≤-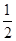 (3)k=±
(3)k=±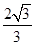
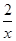 (2)k<0 x≤-
(2)k<0 x≤-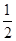 (3)k=±
(3)k=±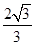
解:(1)因为k=-2,所以A(1,-2),
设反比例函数为y=
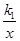 ,因为点A在函数的图象上,所以-2=
,因为点A在函数的图象上,所以-2=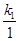 ,
,解得k1=-2,
反比例函数解析式为y=-
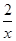 .
.(2)由y=k(x2+x-1)=k
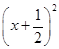 -
-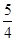 k,得抛物线对称轴为直线x=-
k,得抛物线对称轴为直线x=-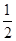 ,
,当k>0时,反比例函数不存在y随着x的增大而增大的取值范围,所以k<0,
此时,当x<0或x>0时,反比例函数值y随着x的增大而增大;
当x≤-
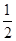 时,二次函数值y随着x的增大而增大,所以自变量x的取值范围是x≤-
时,二次函数值y随着x的增大而增大,所以自变量x的取值范围是x≤-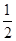 .
.(3)由题(2)得点Q的坐标为
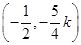 ,
,因为AQ⊥BQ,点O是AB的中点,
所以OQ=
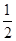 AB=OA,
AB=OA,得
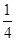 +
+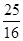 k2=12+k2,解得k=±
k2=12+k2,解得k=±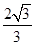 .
.
练习册系列答案
相关题目