题目内容
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
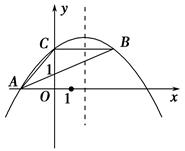
(1)求抛物线的对称轴;
(2)写出A,B,C三点的坐标并求抛物线的解析式.

(1)求抛物线的对称轴;
(2)写出A,B,C三点的坐标并求抛物线的解析式.
(1) 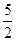 (2) A(-3,0) B(5,4) C(0,4),y=-
(2) A(-3,0) B(5,4) C(0,4),y=-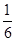 x2+
x2+ x+4
x+4
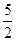 (2) A(-3,0) B(5,4) C(0,4),y=-
(2) A(-3,0) B(5,4) C(0,4),y=-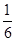 x2+
x2+ x+4
x+4解:(1)抛物线的对称轴为x=-
 =
=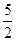 .
.(2)在抛物线y=ax2-5ax+4中,
令x=0,则y=4,∴C点坐标为(0,4).
又∵抛物线的对称轴为x=
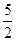 ,B、C两点对称,
,B、C两点对称,∴B点坐标为(5,4).
∵BC=AC,∴AC=BC=5,
∴OA=
 =
=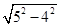 =3,
=3,∴A点坐标为(-3,0).
将A点坐标代入y=ax2-5ax+4,
解得a=-
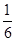 ,∴y=-
,∴y=-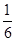 x2+
x2+ x+4.
x+4.
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
 的顶点在x轴上,则c的值为
的顶点在x轴上,则c的值为
 (x-4)2+3,由此可知铅球推出的距离是________m.
(x-4)2+3,由此可知铅球推出的距离是________m.
