题目内容
若1＜x＜3，则|x-1|-|x-3|=________．
2x-4
分析：由x的范围判断出x-1大于0，x-3小于0，利用绝对值的代数意义：正数的绝对值等于它本身；负数的绝对值等于它的相反数；0的绝对值还是0进行化简，去括号合并后即可得到结果．
解答：∵1＜x＜3，
∴x-1＞0，x-3＜0，
则|x-1|-|x-3|=x-1-[-（x-3）]=x-1+x-3=2x-4．
故答案为：2x-4
点评：此题考查了整式的加减运算，以及绝对值的代数意义，根据x的范围化简绝对值运算是解本题的关键．
分析：由x的范围判断出x-1大于0，x-3小于0，利用绝对值的代数意义：正数的绝对值等于它本身；负数的绝对值等于它的相反数；0的绝对值还是0进行化简，去括号合并后即可得到结果．
解答：∵1＜x＜3，
∴x-1＞0，x-3＜0，
则|x-1|-|x-3|=x-1-[-（x-3）]=x-1+x-3=2x-4．
故答案为：2x-4
点评：此题考查了整式的加减运算，以及绝对值的代数意义，根据x的范围化简绝对值运算是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
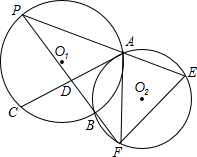、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
已知△ABC中，D是AB上一点，∠BCD=∠A，若BD=1，AD=2，则BC=