题目内容
在△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=8,BC=6,则ED=分析:由题意,作出图形,如图所示,运用勾股定理先求AB的长;利用△ABC面积求得DC的长;运用勾股定理BD长可求;利用中线求BE的长;从而问题可求.
解答: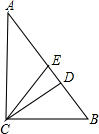 解:∵在△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,
解:∵在△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,
∴BE=
AB,CD⊥AB,
∵AC=8,BC=6,∴AB=
=10,BE=5,
∵
•AC•BC=
•AB•DC,
∴DC=8×6÷10=4.8.
在△BDC中,BD=
=
=3.6,
∴DE=BE-BD=5-3.6=1.4.
 解:∵在△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,
解:∵在△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,∴BE=
| 1 |
| 2 |
∵AC=8,BC=6,∴AB=
| AC2+BC2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴DC=8×6÷10=4.8.
在△BDC中,BD=
| BC2-CD2 |
| 62-(4.8)2 |
∴DE=BE-BD=5-3.6=1.4.
点评:本题考查三角形中线段的求法,解答难度适中.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=