题目内容
矩形ABCD中，若AD=1，AB=| 3 |
分析：依题意画出图形，解出∠BAC，∠ABD的度数，再解出两条对角线所成的锐角．
解答：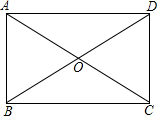
解：如图．
∵tan∠BAC=
=
，
∴∠BAC=30°．
同理∠ABD=30°．
故∠AOD=60°
即这个矩形的两条对角线所成的锐角是60°．
解：如图．∵tan∠BAC=
| BC |
| AB |
| 1 | ||
|
∴∠BAC=30°．
同理∠ABD=30°．
故∠AOD=60°
即这个矩形的两条对角线所成的锐角是60°．
点评：考查了解直角三角形中三角函数的应用．注意特殊角的三角函数值．
练习册系列答案
相关题目
如图，矩形ABCD中，若AB=4，BC=9，E、F分别为BC，DA上的
点，则S四边形AECF等于（ ）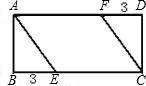
| 1 |
| 3 |
| A、12 | B、24 | C、36 | D、48 |
如图，矩形ABCD中，若AD=1，AB=| 3 |
| A、30° | B、45° |
| C、60° | D、75° |
如图，在矩形ABCD中，若∠AOD=120°，AC=1，则AB=