题目内容
如图,⊙O1和⊙O2相交于A、B两点,⊙O1的弦AC与⊙O2相切,P是 | AmC |
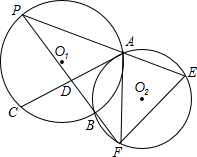 、PB的延长线分别交⊙O2于点E、F,PB交AC于D.
、PB的延长线分别交⊙O2于点E、F,PB交AC于D.(1)求证:PC∥AF;
(2)求证:AE•PC=BE•PD;
(3)若A是PE的中点,则⊙O1与⊙O2是否是等圆?若不是等圆,请说明理由;若是等圆,请给出证明.
分析:(1)欲证PC∥AF,可以证明∠AFB=∠CPB.
(2)欲证AE•PC=BE•PD,即AE:BE=PD:PC,可以证明∠FPC=∠AEB,∠PDC=∠EAB,从而证明△PCD∽△EBA得出;
(3)⊙O1与⊙O2是否是等圆,即直径是否相等.A是PE的中点,可以证明PB,EB分别是⊙O1,⊙O2的直径,它们所在的直角三角形中两直角边分别相等,得出PB=BE,⊙O1与⊙O2是等圆.
(2)欲证AE•PC=BE•PD,即AE:BE=PD:PC,可以证明∠FPC=∠AEB,∠PDC=∠EAB,从而证明△PCD∽△EBA得出;
(3)⊙O1与⊙O2是否是等圆,即直径是否相等.A是PE的中点,可以证明PB,EB分别是⊙O1,⊙O2的直径,它们所在的直角三角形中两直角边分别相等,得出PB=BE,⊙O1与⊙O2是等圆.
解答: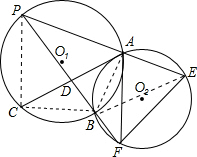 (1)证明:连接AB,PC.
(1)证明:连接AB,PC.
∵AC与⊙O2相切,∴∠CAB=∠AFB.
∵∠CPB=∠CAB,∴∠AFB=∠CPB.
∴PC∥AF;
(2)证明:连BE,BC,
∵PC∥AF,∴∠CPD=∠AFP.
∵∠AFB=∠AEB,∴∠FPC=∠AEB.
∵∠PDC=∠ACB+∠CBD,∠EAB=∠APD+∠ABP,∠ACB=∠APD,∠CBD=∠ABP,
∴∠PDC=∠EAB.
∴△PCD∽△EBA.
∴PC:PD=EB:EA,
∴AE•PC=BE•PD;
(3)解:AC与⊙O2相切,∠CAF=∠E,P是
的中点,
∴∠PAC=∠PCA.
∵PC∥AF,∴∠PCA=∠CAF.
∴∠PAC=∠E.
∴AC∥EF.
∵A是PE的中点,∴PA=EA.
∴AD=CD.
∴四边形PCFA是平行四边形.
∴AF=PC,PA=AE=AF.
∴∠BFE=90°.∴∠BAE=90°=∠BAP.
∴PB,EB分别是⊙O1,⊙O2的直径.
∴PB=BE,⊙O1与⊙O2是等圆.
 (1)证明:连接AB,PC.
(1)证明:连接AB,PC.∵AC与⊙O2相切,∴∠CAB=∠AFB.
∵∠CPB=∠CAB,∴∠AFB=∠CPB.
∴PC∥AF;
(2)证明:连BE,BC,
∵PC∥AF,∴∠CPD=∠AFP.
∵∠AFB=∠AEB,∴∠FPC=∠AEB.
∵∠PDC=∠ACB+∠CBD,∠EAB=∠APD+∠ABP,∠ACB=∠APD,∠CBD=∠ABP,
∴∠PDC=∠EAB.
∴△PCD∽△EBA.
∴PC:PD=EB:EA,
∴AE•PC=BE•PD;
(3)解:AC与⊙O2相切,∠CAF=∠E,P是
 |
| AmC |
∴∠PAC=∠PCA.
∵PC∥AF,∴∠PCA=∠CAF.
∴∠PAC=∠E.
∴AC∥EF.
∵A是PE的中点,∴PA=EA.
∴AD=CD.
∴四边形PCFA是平行四边形.
∴AF=PC,PA=AE=AF.
∴∠BFE=90°.∴∠BAE=90°=∠BAP.
∴PB,EB分别是⊙O1,⊙O2的直径.
∴PB=BE,⊙O1与⊙O2是等圆.
点评:考查了平行线的判断,相似三角形的判定和性质,圆的知识.此题是一个大综合题,难度较大.

练习册系列答案
相关题目
 20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.
20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.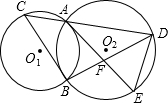 长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点. 16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC.
16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC. (2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.
(2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.