题目内容
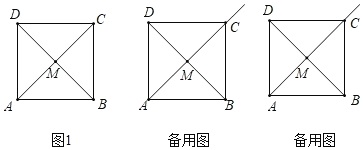
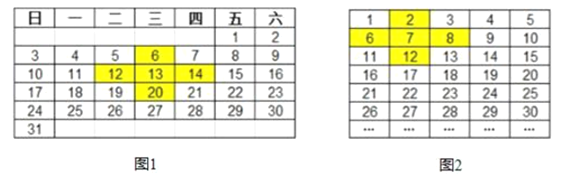
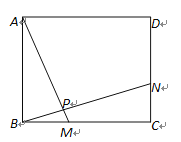
【题目】(1)如图1,已知正方形ABCD,点M和N分别是边BC,CD上的点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论;
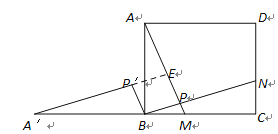
(2)如图2,将图(1)中的△APB绕着点B逆时针旋转90,得到△A′P′B,延长A′P′交AP于点E,试判断四边形BPEP′的形状,并说明理由.
【答案】(1)AM⊥BN,证明见解析;(2)四边形BPEP′是正方形,理由见解析.
【解析】
(1)易证△ABM≌△BCN,再根据角度的关系得到∠APB=90°,即可得到AM⊥BN;
(2)根据旋转的性质及(1)得到四边形BPEP′是矩形,再根据BP= BP′,得到四边形BPEP′是正方形.
(1)AM⊥BN
证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABM=∠BCN=90°
∵BM=CN,
∴△ABM≌△BCN
∴∠BAM=∠CBN
∵∠CBN+∠ABN=90°,
∴∠ABN+∠BAM=90°,
∴∠APB=90°
∴AM⊥BN.
(2)四边形BPEP′是正方形.
△A′P′B是△APB绕着点B逆时针旋转90所得,
∴BP= BP′,∠P′BP=90.
又由(1)结论可知∠APB=∠A′P′B=90°,
∴∠BP′E=90°.
所以四边形BPEP′是矩形.
又因为BP= BP′,所以四边形BPEP′是正方形.

练习册系列答案
相关题目