题目内容
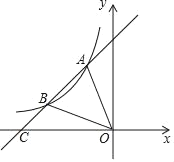
【题目】如图：在数轴上A点表示数
，B点示数
，C点表示数
，是最小的正整数，且、满足
．
（1）=__________，=__________，=__________；
（2）若将数轴折叠，使得A点与C点重合，则点B与数__________表示的点重合；
（3）若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动，假设
秒钟过后，A、B、C三点中恰有一点为另外两点的中点，求的值；
（4）若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时，小聪同学发现：当点C在B点右侧时，
BC+3AB的值是个定值，求此时
的值．
【答案】（1）
=-3，
=1，
=9；（2）5；（3）1, 16, 4；（4）
=1．
【解析】
试题（1）根据非负数的意义求出a、c的值，根据最小的正整数求出b；
（2）根据对称性可求解；
（3）分别以A、B、C为中点，分别求解即可；
（4）分别求出此时的BC、AB的长，然后由
BC+3AB可代入相应的速度值求解是定值的m.
试题解析：（1）因为b是最小的正整数，可得b=1，
根据
，求得=-3，=9；
（2）根据对称性可求解：（-3+9）×2=3,
3-1=2,
3+2=5
答案为：5．
（3）B为中点时，
，
解得
=1,
A为中点时，
解得=16,
C为中点时，
解得=4；
（4）由题意可知，AB=4+t，
BC=8-3t
所以m·BC+3AB
=m·（8-3t）+3（4+t）
=8m+12-（3m-3）t
由定值可知3m-3=0
解得=1．
练习册系列答案
智能训练练测考系列答案
相关题目
