题目内容
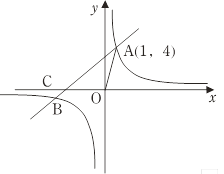
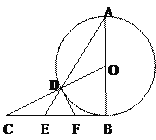
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
【答案】(1)解:∵AB是⊙O的直径,BC是⊙O的切线∴AB⊥BC,
设⊙O的半径为![]() ,在Rt△OBC中,∵
,在Rt△OBC中,∵![]()
∴![]() ,解得
,解得![]() =1,∴⊙O的半径为1
=1,∴⊙O的半径为1
(2)连结OF,∵OA=OB,BF=EF,∴OF∥AE,∠A=∠2
又∵∠BOD=2∠A,∴∠1=∠2,
又∵OB=OD、OF=OF∴△OBF≌△ODF,
∴∠ODF=∠OBF=900,即OD⊥DF,∴FD是⊙O的切线。
【解析】(1)先设⊙O的半径为r,由于AB是⊙O的直径,BC是⊙O的切线,根据切线性质可知AB⊥BC,在Rt△OBC中,利用勾股定理可得![]() ,解得r=1;
,解得r=1;
(2)连接OF,由于OA=OB,BF=EF,可知OF是△BAE的中位线,那么OF∥AE,于是∠A=∠2,根据三角形外角性质可得∠BOD=2∠A,易证∠1=∠2,而OD=OB,OF=OF,利用SAS可证△OBF≌△ODF,那么∠ODF=∠OBF=90°,于是OD⊥DF,从而可证FD是⊙O的切线.

练习册系列答案
相关题目