题目内容
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,﹣3),其顶点为D.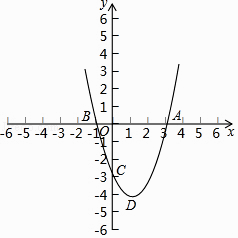
(1)求这个二次函数的解析式及顶点坐标;
(2)在y轴上找一点P(点P与点C不重合),使得∠APD=90°,求点P的坐标;
(3)在(2)的条件下,将△APD沿直线AD翻折得到△AQD,求点Q的坐标.
【答案】
(1)
解:由题意得二次函数图象的对称轴x=1,则﹣ ![]() =1,b=﹣2.
=1,b=﹣2.
又二次过点C(0,﹣3),
∴﹣3=c,c=﹣3.
即二次函数解析式为:y=x2﹣2x﹣3
由y=x2﹣2x﹣3=(x﹣1)2﹣4,得
顶点坐标D为:(1,﹣4);
(2)
解:解法一:设P(0,m)
由题意,得PA= ![]() ,PD=
,PD= ![]() ,AD=2
,AD=2 ![]() ,
,
∵∠APD=90°,∴PA2+PD2=AD2,即( ![]() )2+(
)2+( ![]() )2=(2
)2=(2 ![]() )2
)2
解得m1=﹣1,m2=﹣3(不合题意,舍去).
∴P(0,﹣1);
解法二:
如图,作DE⊥y轴,垂足为点E,
则由题意,得 DE=1,OE=4…
由∠APD=90°,得∠APO+∠DPE=90°,
由∠AOP=90°,得∠APO+∠OAP=90°,
∴∠OAP=∠EPD
又∠AOP=∠OED=90°,
∴△OAP∽△EPD
∴ ![]() =
= ![]() ,
,
设OP=m,PE=4﹣m
则 ![]() =
= ![]() ,
,
解得m1=1,m2=3(不合题意,舍去),
∴P(0,﹣1);

(3)
解:解法一:
如图,作QH⊥x轴,垂足为点H,易得PA=AQ=PD=QD= ![]() ,∠PAQ=90°,
,∠PAQ=90°,
∴四边形APDQ为正方形.
由∠QAP=90°,得∠HAQ+∠OAP=90°,由∠AOP=90°,得∠APO+∠OAP=90°,
∴∠OPA=∠HAQ,又∠AOP=∠AHQ=90°,PA=QA
∴△AOP≌△AHQ,
∴AH=OP=1,QH=OA=3.
∴Q(4,﹣3);

解法二:
设Q(m,n),
则AQ= ![]() =
= ![]() ,QD=
,QD= ![]() =
= ![]() ,
,
解得 ![]() ,
, ![]() (不合题意,舍去),
(不合题意,舍去),
∴Q(4,﹣3).
【解析】(1)根据对称轴的定义求得b=﹣2,把点C的坐标代入求得c=﹣3;将一般式方程转化为顶点式方程即可得到点D的坐标;(2)设P(0,m),由勾股定理分别表示PA,PD,AD的长,由于∠APD=90°,在Rt△PAD中,由勾股定理列方程求m的值即可;(3)作QH⊥x轴,垂足为点H,由勾股定理求出PA=PD= ![]() ,又∠PAQ=90°,可证△PAD为等腰直角三角形,由翻折的性质可知四边形APDQ为正方形,得出△AOP≌△AHQ,利用线段相等关系求Q点坐标.
,又∠PAQ=90°,可证△PAD为等腰直角三角形,由翻折的性质可知四边形APDQ为正方形,得出△AOP≌△AHQ,利用线段相等关系求Q点坐标.

【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8;乙:9,6,10,8,7;
![]() 将下表填写完整:
将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | ______ | 8 | ______ |
乙 | 8 | ______ | 2 |
![]() 根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
![]() 若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______
若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______![]() 填“变大”或“变小”或“不变”
填“变大”或“变小”或“不变”![]()