题目内容
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8;乙:9,6,10,8,7;
![]() 将下表填写完整:
将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | ______ | 8 | ______ |
乙 | 8 | ______ | 2 |
![]() 根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
![]() 若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______
若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______![]() 填“变大”或“变小”或“不变”
填“变大”或“变小”或“不变”![]()
【答案】8;0.4;8;变小
【解析】分析:(1)依据平均数、中位数依据方差的计算方法进行计算;
(2)依据甲的成绩较稳定,即可得到结论;
(3)求得乙这六次射击成绩的方差,即可得到变化情况.
详解:(1)甲平均数为(8+7+9+8+8)÷5=8,
甲的方差为:![]() [(8-8)2+(7-8)2+(9-8)2+(8-8)2+(8-8)2]=0.4,
[(8-8)2+(7-8)2+(9-8)2+(8-8)2+(8-8)2]=0.4,
乙的环数排序后为:6,7,8,9,10,故中位数为8;
故答案为:8,0.4,8;
(2)选择甲.理由是甲的成绩较稳定.
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差为:![]() [(9-8)2+(6-8)2+(10-8)2+(8-8)2+(7-8)2+(8-8)2]=
[(9-8)2+(6-8)2+(10-8)2+(8-8)2+(7-8)2+(8-8)2]=![]() <2,
<2,
∴方差会变小.
故答案为:变小.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
【题目】某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题: 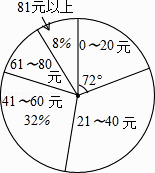
捐款 | 人数 |
0~20元 | |
21~40元 | |
41~60元 | |
61~80元 | 6 |
81元以上 | 4 |
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?