题目内容
△ABC中，∠A=2∠B=75°，则∠C等于
- A.30°
- B.67°30′
- C.60°
- D.77°30′
B
分析：先根据∠A=2∠B=75°，求出∠B的度数，再利用三角形内角和的定理求出∠C的度数．
解答：∵∠A=2∠B=75°，
∴∠B=37°30′．
∵∠A+∠B+∠C=180°，
∴∠C=67°30′．
故选B．
点评：本题利用了三角形内角和为180°．
分析：先根据∠A=2∠B=75°，求出∠B的度数，再利用三角形内角和的定理求出∠C的度数．
解答：∵∠A=2∠B=75°，
∴∠B=37°30′．
∵∠A+∠B+∠C=180°，
∴∠C=67°30′．
故选B．
点评：本题利用了三角形内角和为180°．
练习册系列答案
阅读快车系列答案
相关题目
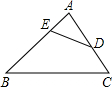如图，在△ABC中，AC=2，AB=3，D是AC上一点，E是AB上一点，且∠ADE=∠B，设AD=x，AE=y，则y与x之间的函数关系式是（ ）A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
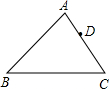如图，在△ABC中，AB=8，AC=6，BC=7，点D在AC上，AD=2，