题目内容
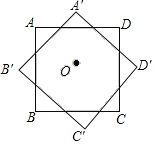
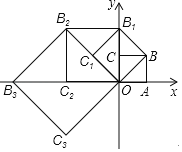
【题目】如图，在平面直角坐标系中，对角线为1的正方形OABC，点A在x轴的正半轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OBlB2C2，照此规律作下去，则点B2019的坐标为（ ）
A.（﹣21009，21009）B.（21008，﹣21008）
C.（﹣21009
，0）D.（0，21008）
【答案】C
【解析】
首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标，找出这些坐标的之间的规律，然后根据规律计算出点B2019的坐标．
∵正方形OABC对角线OB＝1，正方形OBB1C1是正方形OABC的对角线OB为边，
∴OB1＝
，
∴B1点坐标为（0，），
同理可知OB2＝2，B2点坐标为（﹣，），
同理可知OB3＝2，B3点坐标为（﹣2，0），
B4点坐标为（﹣2，﹣2），B5点坐标为（0，﹣4），
B6（4，﹣4），B7（8，0），
B8（8，8），B9（0，16），
由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍，
∵2019÷8＝252…3，
∴B2019的纵横坐标符号与点B3的相同，横坐标为负值，纵坐标是0，
∴B2019的坐标为（﹣21009，0）．
故选C．
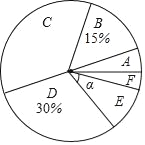
【题目】在星期一的第八节课，我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试，并对成绩进行统计分析，绘制了频数分布表和统计图，按得分划分成A、B、C、D、E、F六个等级，并绘制成如下两幅不完整的统计图表．
等级 | 得分x（分） | 频数（人） |
A | 95＜x≤100 | 4 |
B | 90＜x≤95 | m |
C | 85＜x≤90 | n |
D | 80＜x≤85 | 24 |
E | 75＜x≤80 | 8 |
F | 70＜x≤75 | 4 |
请你根据图表中的信息完成下列问题：
1）本次抽样调查的样本容量是 ．其中m= ，n= ．
2）扇形统计图中，求E等级对应扇形的圆心角α的度数；
3）我校九年级共有700名学生，估计体育测试成绩在A、B两个等级的人数共有多少人？
4）我校决定从本次抽取的A等级学生（记为甲、乙、丙、丁）中，随机选择2名成为学校代表参加全市体能竞赛，请你用列表法或画树状图的方法，求恰好抽到甲和乙的概率．
