题目内容
【题目】在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.过射线AD上一点M作BM的垂线,交直线AC于点N.
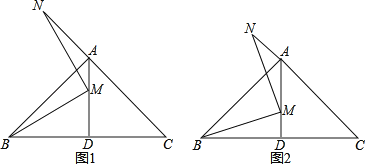
(1)如图1,点M在AD上,若∠N=15°,BC=2![]() ,则线段AM的长为 ;
,则线段AM的长为 ;
(2)如图2,点M在AD上,求证:BM=NM;
(3)若点M在AD的延长线上,则AB,AM,AN之间有何数量关系?直接写出你的结论,不证明.
【答案】(1)![]() ﹣1;(2)见解析;(3)
﹣1;(2)见解析;(3)![]() AM.
AM.
【解析】
(1)证得∠ABM=15°,则∠MBD=30°,求出DM=1,则AM可求出;
(2)过点M作AD的垂线交AB于点E,根据ASA可证明△BEM≌△NAM,得出BM=NM;
(3)过点M作AD的垂线交AB于点E,同(2)可得△AEM为等腰直角三角形,证明△BEM≌△NAM,BE=AN,则问题可解;
解:(1)∵∠N=15°,∠BMN=∠BAN=90°,
∴∠ABM=15°,
∵AB=AC,∠BAC=90°,AD⊥BC,
∴∠ABC=∠C=45°,BD=CD,
∴∠MBD=∠ABD﹣∠ABM=45°﹣15°=30°.
∴DM=![]() .
.
∴![]() ﹣1.
﹣1.
故答案为:![]() ﹣1;
﹣1;
(2)过点M作AD的垂线交AB于点E,
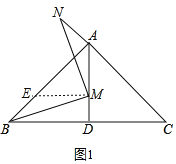
∵∠BAC=90°,AB=AC,AD⊥BC,
∴∠NAB=90°,∠BAD=45°,
∴∠AEM=90°﹣45°=45°∠BAD,
∴EM=AM,∠BEM=135°,
∵∠NAB=90°,∠BAD=45°,
∴∠NAD=135°,
∴∠BEM=∠NAD,
∵EM⊥AD,
∴∠AMN+∠EMN=90°,
∵MN⊥BM,
∴∠BME+∠EMN=90°,
∴∠BME=∠AMN,
在△BEM和△NAM中,
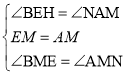 ,
,
∴△BEM≌△NAM(ASA),
∴BM=NM;
(3)数量关系是:AB+AN=![]() AM.
AM.
证明:过点M作AD的垂线交AB于点E,
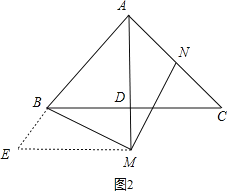
同(2)可得△AEM为等腰直角三角形,
∴∠E=45°,AM=EM,
∵∠AME=∠BMN=90°,
∴∠BME=∠AMN,
在△BEM和△NAM中,
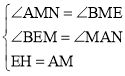 ,
,
∴△BEM≌△NAM(AAS),
∴BE=AN,
∴![]() AM.
AM.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案