题目内容
【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB.
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2, 求阴影部分面积.
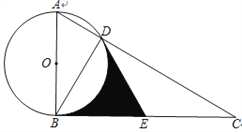
【答案】(1)证明见解析;
(2)∠BOD=120°;
(3)S阴影部分=![]()
【解析】试题分析:(1)、连接OD,根据直径得出∠BDC=90°,根据直角三角形斜边上的中线的性质得出∠BDE=∠DBE,根据OD=OB得出∠ODB=∠OBD,从而得出∠ODE为直角,得出切线;(2)、根据直角三角形的性质得出∠DEB=60°,根据四边形OBED的内角和得出∠BOD的度数;(3)、根据阴影部分的面积等于四边形OBED的面积减去扇形OBD的面积得出答案.
试题解析:(1)连结OD,∵AB为⊙O为直径 ∴∠ADB=90°则∠BDC=90°,
又∵E是斜边BC的中点 ∴DE=BE=CE, ∴∠BDE=∠DBE
∵OD=OB,∴∠ODB=∠OBD
∴∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°
即DE与⊙O相切
(2)若∠C=30°而DE=CE ∴∠DEB=60°
在四边形OBED中, 则∠BOD=360°-90°-90°-60°=120°
(3)连结OE,则∠OED=∠OEB=30°
∵OD=OB=2 ∴DE=BE=2![]()
∴S阴影部分=S四边形OBED-S扇形OBD=S△OBE+S△ODE-S扇形OBD
=2![]() +2
+2![]() -
-![]() =4
=4![]() -
-![]()

练习册系列答案
相关题目