题目内容
【题目】如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,…的顶点B1,B2,B3,…在x轴上,顶点C1,C2,C3,…在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3,则点C3的纵坐标是______________.
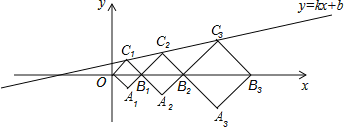
【答案】![]()
【解析】
连接A1C1,A2C2,A3C3,分别交x轴于点E、F、G.根据正方形的性质,由OB1=2,B1B2=3可求点C1,C2的坐标,将点C1,C2的坐标代入y=kx+b中,得到关于k与b的方程组,求出方程组的解得到k与b的值,从而求出直线解析式,设B2G=C3G=t,表示出C3的坐标,代入直线方程中列出关于t的方程,求出方程的解得到t的值,确定出C3的纵坐标.
解:如图,连接A1C1,A2C2,A3C3,分别交x轴于点E、F、G,
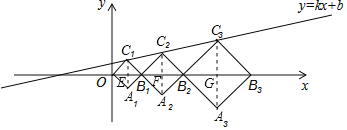
∵四边形OA1B1C1,B1A2B2C2,B2A3B3C3都是正方形,OB1=2,B1B2=3,
∴OE=EC1=EB1=![]() OB1=1,B1F=FC2=FB2=
OB1=1,B1F=FC2=FB2=![]() B1B2=
B1B2=![]() ,OF=OB1+B1F=
,OF=OB1+B1F=![]() ,
,
∴C1(1,1),C2(![]() ,
,![]() ),
),
将点C1,C2的坐标代入y=kx+b中,
得: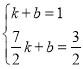 ,解得:
,解得:![]() ,
,
∴直线解析式为y=![]() x+
x+![]() ,
,
设B2G=C3G=t,则有C3坐标为(5+t,t),
代入直线解析式得:t=![]() (5+t)+
(5+t)+![]() ,
,
解得:t=![]() ,
,
∴点C3的纵坐标是![]() .
.
故答案是![]() .
.

练习册系列答案
相关题目