题目内容
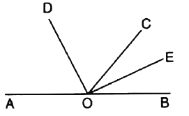
【题目】如图,点A、B在同一条直线上,OD、OE分别平分∠AOC和∠BOC.(1)求∠DOE的度数；(2)如果∠COD=65°,求∠AOE的度数.
【答案】（1）90°；（2）155°．
【解析】
（1）由已知条件和观察图形，再利用角平分线的性质就可求出角的度数；
（2）由已知条件和观察图形，再利用角平分线的性质就可求出角的度数．
解：（1）如图，因为OD是∠AOC的平分线，
所以∠COD=
∠AOC，
又因为OE是∠BOC的平分线，
所以∠COE=∠BOC．
所以∠DOE=∠COD+∠COE=（∠AOC+∠BOC）=∠AOB=90°．
（2）由（1）可知，∠BOE=∠COE=90°-∠COD=25°．
所以∠AOE=∠AOB-∠BOE=155°．
故答案为：（1）90°；（2）155°．
口算题卡北京妇女儿童出版社系列答案
【题目】某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，如果期末评价成绩80分以上（含80分），则评为“优秀”．下面表中是小张和小王两位同学的成绩记录：
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
（1）若按三项成绩的平均分记为期末评价成绩，请计算小张的期末评价成绩；
（2）若按完成作业、单元检测、期末考试三项成绩按
的权重来确定期末评价成绩．
①请计算小张的期末评价成绩为多少分？
②小王在期末（期末成绩为整数）应该最少考多少分才能达到优秀？
【题目】一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元．设购进A型
手机x部，B型手机y部．三款手机的进价和预售价如下表：
手机型号 | A型 | B型 | C型 |
进 价（单位：元/部） | 900 | 1200 | 1100 |
预售价（单位：元/部） | 1200 | 1600 | 1300 |
（1）用含x，y的式子表示购进C型手机的部数；
（2）求出y与x之间的函数关系式；
（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
①求出预估利润P（元）与x（部）的函数关系式；
（注：预估利润P＝预售总额-购机款-各种费用）
②求出预估利润的最大值，并写出此时购进三款手机各多少部．
