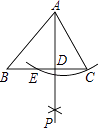ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÎĘĖâąģū°Ģš
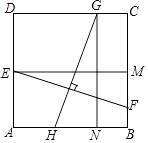
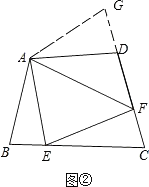
ČįÍžĒŲĢŽÔÚËÄąßÐÎABCDÖÐĢŽAB=ADĢŽĄÏBAD=120ĄãĢŽĄÏB=ĄÏADC=90ĄãĢŽEĢŽF·ÖąðĘĮBCĄĒCDÉÏĩÄĩãĢŽĮŌĄÏEAF=60ĄãĢŪĖ―ūŋÍžÖÐÏßķÎBEĢŽEFĢŽFDÖŪžäĩÄĘýÁŋđØÏĩĢŪ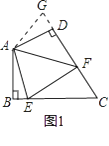
ĢĻ1ĢĐÐĄÃũÍŽŅ§Ė―ūŋīËÎĘĖâĩÄ·―·ĻĘĮĢŽŅÓģĪFDĩ―ĩãGĢŽĘđDG=BEĢŽÁŽ―ÓAGĢŽÏČÖĪÃũĄũABEĄÕADGĢŽÔŲÖĪÃũĄũAEFĄÕĄũAGFĢŽŋÉĩÃģö―áÂÛĢŽËûĩÄ―áÂÛÓĶĘĮĢŧ
ĢĻ2ĢĐĖ―ËũŅÓÉėĢš
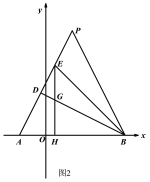
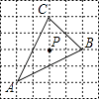
ČįÍžĒÚĢŽČôÔÚËÄąßÐÎABCDÖÐĢŽAB=ADĢŽĄÏB+ĄÏD=180ĄãĢŪEĢŽF·ÖąðĘĮBCĢŽCDÉÏĩÄĩãĢŽĮŌĄÏEAF= ![]() ĄÏBADĢŽÉÏĘö―áÂÛĘĮ·ņČÔČŧģÉÁĒĢŽĮëËĩÃũĀíÓÉĢŧ
ĄÏBADĢŽÉÏĘö―áÂÛĘĮ·ņČÔČŧģÉÁĒĢŽĮëËĩÃũĀíÓÉĢŧ 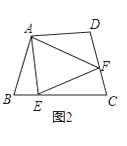
ĢĻ3ĢĐĘĩžĘÓĶÓÃĢš
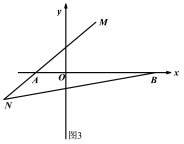
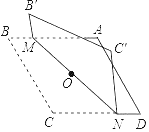
ČįÍžĒÛĢŽÔÚÄģīÎūüĘÂŅÝÏ°ÖÐĢŽ―ĒͧžŨÔÚÖļŧÓÖÐÐÄOąąÆŦÎũ30ĄãĩÄAīĶĢŽ―ĒͧŌŌÔÚÖļŧÓÖÐÐÄÄÏÆŦķŦ70ĄãĩÄBīĶĢŽēĒĮŌÁ――Ēͧĩ―ÖļŧÓÖÐÐÄĩÄūāĀëÏāĩČĢŽ―Óĩ―ÐÐķŊÖļÁîšóĢŽ―ĒͧžŨÏōÕýķŦ·―ÏōŌÔ60šĢĀï/ÐĄĘąĩÄËŲķČĮ°―øĢŽ―ĒͧŌŌŅØąąÆŦķŦ50ĄãĩÄ·―ÏōŌÔ80šĢĀï/ÐĄĘąĩÄËŲķČĮ°―øĢŽ2ÐĄĘąšóĢŽÖļŧÓÖÐÐÄđÛēâĩ―žŨĄĒŌŌÁ――Ēͧ·Öąðĩ―īïEĢŽFīĶĢŽĩąĄÏEOF=70ĄãĘąĢŽÁ――ĒͧÖŪžäĩÄūāĀëĘĮšĢĀïĢŪ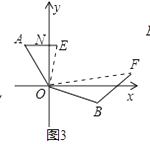
ĢĻ4ĢĐÄÜÁĶĖáļßĢš
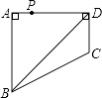
ČįÍžĒÜĢŽĩČŅüÖą―ĮČý―ĮÐÎABCÖÐĢŽĄÏBAC=90ĄãĢŽAB=ACĢŽĩãMĢŽNÔÚąßBCÉÏĢŽĮŌĄÏMAN=45ĄãĢŪČôBM=1ĢŽCN=3ĢŽÔōMNĩÄģĪΊ ĢŪ 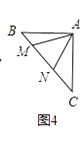
Ąūīð°ļĄŋ
ĢĻ1ĢĐEF=BE+DF
ĢĻ2ĢĐ
―âĢš―áÂÛEF=BE+DFČÔČŧģÉÁĒĢŧ
ĀíÓÉĢšŅÓģĪFDĩ―ĩãGĢŪĘđDG=BEĢŪÁŽ―áAGĢŽČįÍžĒÚĢŽ
ÔÚĄũABEšÍĄũADGÖÐĢŽ 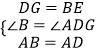 ĢŽ
ĢŽ
ĄāĄũABEĄÕĄũADGĢĻSASĢĐĢŽ
ĄāAE=AGĢŽĄÏBAE=ĄÏDAGĢŽ
ĄßĄÏEAF= ![]() ĄÏBADĢŽ
ĄÏBADĢŽ
ĄāĄÏGAF=ĄÏDAG+ĄÏDAF=ĄÏBAE+ĄÏDAF=ĄÏBADĐĄÏEAF=ĄÏEAFĢŽ
ĄāĄÏEAF=ĄÏGAFĢŽ
ÔÚĄũAEFšÍĄũGAFÖÐĢŽ 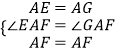 ĢŽ
ĢŽ
ĄāĄũAEFĄÕĄũAGFĢĻSASĢĐĢŽ
ĄāEF=FGĢŽ
ĄßFG=DG+DF=BE+DFĢŽ
ĄāEF=BE+DFĢŧ
ĢĻ3ĢĐ280
ĢĻ4ĢĐ![]()
Ąū―âÎöĄŋ―âĢšĢĻ1.ĢĐEF=BE+DFĢŽÖĪÃũČįÏÂĢš
ÔÚĄũABEšÍĄũADGÖÐĢŽ 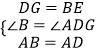 ĢŽ
ĢŽ
ĄāĄũABEĄÕĄũADGĢĻSASĢĐĢŽ
ĄāAE=AGĢŽĄÏBAE=ĄÏDAGĢŽ
ĄßĄÏEAF= ![]() ĄÏBADĢŽ
ĄÏBADĢŽ
ĄāĄÏGAF=ĄÏDAG+ĄÏDAF=ĄÏBAE+ĄÏDAF=ĄÏBADĐĄÏEAF=ĄÏEAFĢŽ
ĄāĄÏEAF=ĄÏGAFĢŽ
ÔÚĄũAEFšÍĄũGAFÖÐĢŽ 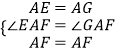 ĢŽ
ĢŽ
ĄāĄũAEFĄÕĄũAGFĢĻSASĢĐĢŽ
ĄāEF=FGĢŽ
ĄßFG=DG+DF=BE+DFĢŽ
ĄāEF=BE+DFĢŧ
ËųŌÔīð°ļĘĮ EF=BE+DFĢŪ
ĢĻ3.ĢĐČįÍžĒÛĢŽÁŽ―ÓEFĢŽŅÓģĪAEĄĒBFÏā―ŧÓÚĩãCĢŽ
ĄßĄÏAOB=30Ąã+90Ąã+ĢĻ90ĄãĐ70ĄãĢĐ=140ĄãĢŽĄÏEOF=70ĄãĢŽ
ĄāĄÏEOF= ![]() ĄÏAOBĢŽ
ĄÏAOBĢŽ
ÓÖĄßOA=OBĢŽĄÏOAC+ĄÏOBC=ĢĻ90ĄãĐ30ĄãĢĐ+ĢĻ70Ąã+50ĄãĢĐ=180ĄãĢŽ
Ąā·ûšÏĖ―ËũŅÓÉėÖÐĩÄĖõžþĢŽ
Ąā―áÂÛEF=AE+BFģÉÁĒĢŽ
žīEF=2ĄÁĢĻ60+80ĢĐ=280šĢĀïĢŪ
īðĢšīËĘąÁ――ĒͧÖŪžäĩÄūāĀëĘĮ280šĢĀïĢŧ
ËųŌÔīð°ļĘĮĢš280Ģŧ
ĢĻ4.ĢĐČįÍž4ĢŽ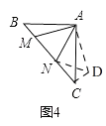
―ŦĄũABMČÆĩãAÄæĘąÕëÐýŨŠĩÃĩ―ĄũACDĢŽ
ĄāĄũABMĄÕĄũACDĢŽ
ĄāĄÏAMB=ĄÏADCĢŽĄÏBAM=ĄÏCAMĢŽAM=ADĢŽBM=CD=1ĢŽ
ĄßĄÏAMB+ĄÏAMC=90ĄãĢŽ
ĄāĄÏAMC+ĄÏADC=180ĄãĢŽ
ĄāĄÏMAD+ĄÏMCD=180ĄãĢŽ
ĄßĄÏBAC=90ĄãĢŽ
ĄāĄÏMAD=ĄÏMAC+ĄÏCAD=ĄÏMAC+ĄÏBAM=90ĄãĢŽ
ĄāĄÏMCD=90ĄãĢŽ
ÔÚRtĄũNCDÖÐĢŽCN=3ĢŽCD=1ĢŽ
ļųūÝđīđÉķĻĀíĩÃĢŽND= ![]() ĢŽ
ĢŽ
ĄßĄÏMAD=90ĄãĢŽĄÏMAN=45ĄãĢŽ
ĄāĄÏDAN=45ĄãĢŽ
ĄßAM=ADĢŽAN=ANĢŽ
ĄāĄũMANĄÕĄũDANĢŽ
ĄāMN=DN= ![]() ĢŽ
ĢŽ
ËųŌÔīð°ļĘĮ ![]() ĢŪ
ĢŪ
ĄūŋžĩãūŦÎöĄŋČÏÕæÉóĖâĢŽĘŨÏČÐčŌŠÁË―âČŦĩČČý―ĮÐÎĩÄÐÔÖĘ(ČŦĩČČý―ĮÐÎĩÄķÔÓĶąßÏāĩČ; ČŦĩČČý―ĮÐÎĩÄķÔÓĶ―ĮÏāĩČ)ĢŪ

 ĀčÃũÎÄŧŊšŪžŲŨũŌĩÏĩÁÐīð°ļ
ĀčÃũÎÄŧŊšŪžŲŨũŌĩÏĩÁÐīð°ļ