Question

【题目】如图，已知锐角三角形ABC，以点A为圆心，AC为半径画弧与BC交于点E，分别以点E、C为圆心，以大于 EC的长为半径画弧相交于点P，作射线AP，交BC于点D．若BC=5，AD=4，tan∠BAD= ，则AC的长为（ ）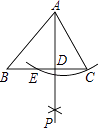
A.3
B.5
C.
D.2

Answer 1

【答案】D
【解析】解：由作图知，AD⊥BC于D， 在Rt△ABD中，AD=4，tan∠BAD= = = ，
∴BD=3，
∵BC=5，
∴CD=BC﹣BD=2，
在Rt△ADC中，AC= =2 ，
故选D．
【考点精析】本题主要考查了解直角三角形的相关知识点，需要掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．