题目内容
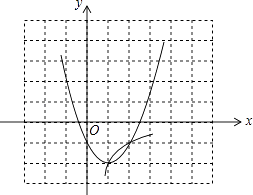
【题目】如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(﹣4,1),点D的坐标为(0,1),点B,P都在反比例函数y= ![]() 的图象上,且P时动点,连接OP,CP.
的图象上,且P时动点,连接OP,CP. 
(1)求反比例函数y= ![]() 的函数表达式;
的函数表达式;
(2)当点P的纵坐标为 ![]() 时,判断△OCP的面积与正方形ABCD的面积的大小关系.
时,判断△OCP的面积与正方形ABCD的面积的大小关系.
【答案】
(1)解:∵四边形ABCD是正方形,A(﹣4,1),D(0,1),
∴OD=1,BC=DC=AD=4,
∴OC=3,
∴点B的坐标为(﹣4,﹣3).
∵点B在反比例函数y= ![]() 的图象上,
的图象上,
∴k=﹣4×(﹣3)=12,
∴反比例函数的表达式为y= ![]() ;
;
(2)解:∵点P在反比例函数y= ![]() 的图象上,点P的纵坐标为
的图象上,点P的纵坐标为 ![]() ,
,
∴点P的横坐标为 ![]() ,
,
∴S△OCP= ![]() ×3×
×3× ![]() =16.
=16.
∵S正方形ABCD=16,
∴△OCP的面积与正方形ABCD的面积相等.
【解析】(1)只需根据条件求出点B的坐标,然后运用待定系数法就可解决问题;(2)易求出OC的长,然后只需根据条件求出点P的横坐标,就可求出△OCP的面积,然后再求出正方形ABCD的面积,就可解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目