题目内容
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
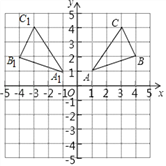
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=![]() S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。

【答案】⑴ A1(-1,1),B1(-4,2),C1(-3,4);(2)P坐标为(2,0);(3)Q(0, ![]() )或(0,
)或(0, ![]() )
)
【解析】试题分析:(1)找出点A、B、C关于y轴的对称点的位置,然后顺次连接即可得到△A1B1C1;
(2),找出A的对称点A′,连接BA′,与x轴交点即为P,从而得到点P的坐标;
(3)作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,根据三角形的面积求出S△ABC,再由S△AOQ=![]() S△ABC解y值即可得到点Q坐标.
S△ABC解y值即可得到点Q坐标.
试题解析:(1)△A1B1C1如图所示,A1(-1,1),B1(-4,2),C1(-3,4);
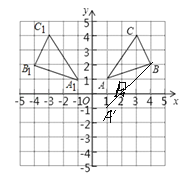
(2)如图1,找出A的对称点A′(1,﹣1),连接BA′,与x轴交点即为P,点P坐标为(2,0);
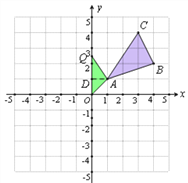
(3)设存在点 Q,使得S△AOQ=![]() S△ABC,如图2,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,
S△ABC,如图2,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,
S△ABC=![]() =
=![]() ,
,
由题意,S△AOQ=![]() S△ABC,得
S△ABC,得 ![]() ,
,
![]() 或
或![]() ,
,
∴ Q点坐标为(0, ![]() )或(0,
)或(0, ![]() ).
).

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目