��Ŀ����
����Ŀ����һ�ο���ѧϰ�л��,��ʦ���������һ������:
��P��������ABCD�ڵ�һ��,����P��ֱ��l�ֱ������ε������ڵ�M��N,ʹ��P���߶�MN�����ȷֵ�,������ֱ���ܹ�������?
����˼��,��ͬѧ�������»���:
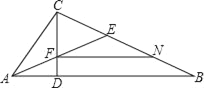
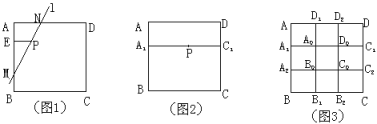
��ͼ1,����P��PE��AB��E,��EB��ȡ��M,ʹEM=2EA,��ֱ��MP��AD��N,��ֱ��MN���Ƿ���������ֱ��l.
����������Ϣ,�����������:
(1)��ͬѧ�Ļ����Ƿ���ȷ?��˵������.
(2)��ͼ1��,�ܷ�������Ŀ������ֱ��?�����,��ֱ����ͼ1�л���.
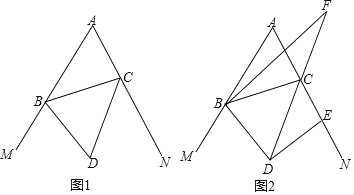
(3)��ͼ2,A1��C1�ֱ���������ABCD�ı�AB��CD�ϵ����ȷֵ�,��A1C1��AD.����P���߶�A1C1��ʱ,�ܷ�������Ŀ������ֱ��?�����,���Ի�������?
(4)��ͼ3,������ABCD�߽��ϵ�A1��A2��B1��B2��C1��C2��D1��D2�������ڱߵ����ȷֵ�.����P��������ABCD�ڵIJ�ͬλ��ʱ,������,������Ŀ������ֱ��l�����������.
���𰸡�(1)��ͬѧ�Ļ�����ȷ�����ɼ�������(2)�ܻ���һ��������Ŀ������ֱ��,ͼ1��(3)����P���߶�A1C1��,�ܹ�����������Ŀ������ֱ��������,ͼ2��(4) ������.
��������
��1��������MPE�ס�MNA�еijɱ����߶ο�֪EM=2EA������MP��MN=2��3������P���߶�MN��һ�����ȷֵ㣻
��2���ɣ�1���е�֤�����̿�֪����EB��ȡM1��ʹEM1=![]() AE��ֱ��M1P��������������ֱ�ߣ������ܻ���һ��������Ŀ������ֱ�ߣ�
AE��ֱ��M1P��������������ֱ�ߣ������ܻ���һ��������Ŀ������ֱ�ߣ�
��3������P���߶�A1C1�ϣ����������ε����ʿ�֪�ܹ�����������Ŀ������ֱ������������
��4����������ۣ�
(1)��ͬѧ�Ļ�����ȷ.
��PE��AD��
����MPE����MNA��
��![]() ��
��
��EM=2EA��
��MP:MN=2:3��
���P���߶�MN��һ�����ȷֵ㣻
(2)�ܻ���һ��������Ŀ������ֱ�ߣ���EB��ȡM1��ʹEM1=![]() AE��ֱ��M1P��������������ֱ�ߣ���ͼ1��
AE��ֱ��M1P��������������ֱ�ߣ���ͼ1��
(3)����P���߶�A1C1�ϣ��ܹ�����������Ŀ������ֱ������������ͼ2��
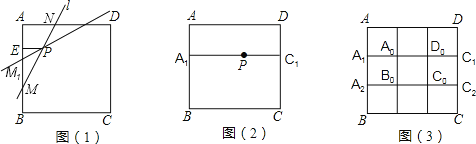
(4)����P��A1C1��A2C2��B1D1��B2D2��ʱ�����Ի�������������������ֱ��l��
����P��������A0B0C0D0�ڲ�ʱ��������������ֱ��l��ʹ�õ�P���߶�MN�����ȷֵ㣻
����P�ھ���ABB1D1��CDD2B2��A0D0D2D1��B0B1B2C0�ڲ�ʱ������P�ɻ�����������������ֱ��l��ʹ�õ�P���߶�MN�����ȷֵ�.

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�