题目内容
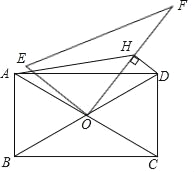
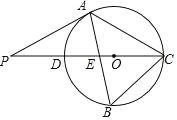
【题目】如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径;
,求⊙O的直径;
(3)在(2)的条件下,若点B等分半圆CD,求DE的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)连接OA、AD,如图,利用圆周角定理得到∠B=∠ADC,则可证明∠ADC=2
∠ACP,利用CD为直径得到∠DAC=90°,从而得到∠ADC=60°,∠C=30°,则∠AOP=60°,
于是可证明∠OAP=90°,然后根据切线的判断定理得到结论;
(2)利用∠P=30°得到OP=2OA,则![]() ,从而得到⊙O的直径;
,从而得到⊙O的直径;
(3)作EH⊥AD于H,如图,由点B等分半圆CD得到∠BAC=45°,则∠DAE=45°,设
DH=x,则DE=2x,![]() 所以
所以![]() 然后求出x即可
然后求出x即可
得到DE的长.
(1)证明:连接OA、AD,如图,
∵∠B=2∠P,∠B=∠ADC,
∴∠ADC=2∠P,
∵AP=AC,
∴∠P=∠ACP,
∴∠ADC=2∠ACP,
∵CD为直径,
∴∠DAC=90°,
∴∠ADC=60°,∠C=30°,
∴△ADO为等边三角形,
∴∠AOP=60°,
而∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:在Rt△OAP中,∵∠P=30°,
∴OP=2OA,
∴![]()
∴⊙O的直径为![]() ;
;
(3)解:作EH⊥AD于H,如图,
∵点B等分半圆CD,
∴∠BAC=45°,
∴∠DAE=45°,
设DH=x,
在Rt△DHE中,DE=2x,![]()
在Rt△AHE中,![]()
∴![]()
即![]()
解得![]()
∴![]()

【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?