题目内容
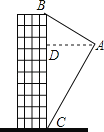
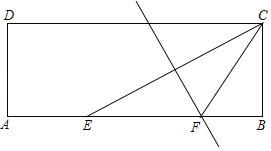
【题目】如图,在矩形ABCD中,AB=3BC,以点A为圆心,AD为半径画弧交AB于点E连接CE,作线段CE的中垂线交AB于点F,连接CF,则sin∠CFB=_____.
【答案】![]()
【解析】
设BF=x,AD=BC=a,则AB=3BC=3a,AE=AD=a,则BE=AB﹣AE=3a﹣a=2a,因为CE的中垂线交AB于点F,所以EF=FC=2a﹣x,在Rt△CBF中,BF2+BC2=CF2,即x2+a2=(2a﹣x)2,x=![]() ,所以BF=
,所以BF=![]() ,CF=2a﹣
,CF=2a﹣![]() ,然后求解即可.
,然后求解即可.
设BF=x,AD=BC=a,则AB=3BC=3a,AE=AD=a,
∴BE=AB﹣AE=3a﹣a=2a,
∵CE的中垂线交AB于点F,
∴EF=FC=2a﹣x,
在Rt△CBF中,
BF2+BC2=CF2,
即x2+a2=(2a﹣x)2,
x=![]() ,
,
∴BF=![]() ,CF=2a﹣
,CF=2a﹣![]() =
=![]() ,
,
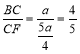 ,
,
故答案为![]() .
.

练习册系列答案
相关题目